如图.正方形ABCD中.P.Q分别是边BC.CD的中点.若$\overrightarrow{AC}$=x$\overrightarrow{AP}$+y$\overrightarrow{BQ}$.则xy=( )A．2B．$\frac{8}{3}$C．$\frac{6}{5}$D．$\frac{12}{25}$ 题目和参考答案——青夏教育精英家教网——

题目内容

17．如图，正方形ABCD中，P，Q分别是边BC，CD的中点，若$\overrightarrow{AC}$=x$\overrightarrow{AP}$+y$\overrightarrow{BQ}$，则xy=（　　）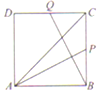

A．

2

B．

$\frac{8}{3}$

C．

$\frac{6}{5}$

D．

$\frac{12}{25}$

分析 $\overrightarrow{AC}=x\overrightarrow{AP}+y\overrightarrow{BQ}=x（\overrightarrow{AB}+\overrightarrow{BP}）+$y（$\overrightarrow{BC}+\overrightarrow{CQ}）$=x（$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$）+y（$\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$）=（x-$\frac{1}{2}y$）$\overrightarrow{AB}$+（$\frac{1}{2}x+y$）$\overrightarrow{AD}$=$\overrightarrow{AB}+\overrightarrow{AD}$．可得x-$\frac{1}{2}y$=1，$\frac{1}{2}x+y$=1，即可

解答解：∵$\overrightarrow{AC}=x\overrightarrow{AP}+y\overrightarrow{BQ}=x（\overrightarrow{AB}+\overrightarrow{BP}）+$y（$\overrightarrow{BC}+\overrightarrow{CQ}）$=x（$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$）+y（$\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$）=（x-$\frac{1}{2}y$）$\overrightarrow{AB}$+（$\frac{1}{2}x+y$）$\overrightarrow{AD}$=$\overrightarrow{AB}+\overrightarrow{AD}$．
可得x-$\frac{1}{2}y$=1，$\frac{1}{2}x+y$=1，解得x=$\frac{6}{5}$，y=$\frac{2}{5}$，∴xy=$\frac{12}{25}$
故选：D

点评本题考查了向量的线性运算，属于中档题．

练习册系列答案

新课标两导两练高效学案系列答案

金榜夺冠系列答案

期末复习百分百系列答案

标准单元测试卷系列答案

名校学案全能测评100分系列答案

天利38套对接中考单元专题双测卷系列答案

全程考评一卷通系列答案

课时金练系列答案

小学同步3练探究100分系列答案

名师点拨测试卷系列答案

相关题目

7．抛物线x=$\frac{1}{4m}$y²的焦点坐标是（m，0）．

8．已知椭圆C₁：$\frac{x^2}{a_1^2}+\frac{y^2}{b_1^2}=1（{a_1}＞{b_1}＞0）$，双曲线C₂：$\frac{x^2}{a_1^2}-\frac{y^2}{b_1^2}=1（{a_2}＞0，{b_2}＞0）$，以C₁的短轴为一条最长对角线的正六边形与x轴正半轴交于点M，F为椭圆右焦点，A为椭圆右顶点，B为直线$x=\frac{a_1^2}{c_1}$与x轴的交点，且满足|OM|是|OA|与|OF|的等差中项，现将坐标平面沿y轴折起，当所成二面角为60°时，点A，B在另一半平面内的射影恰为C₂的左顶点与左焦点，则C₂的离心率为2．

5．一桥拱的形状为抛物线，该抛物线拱的高为h，宽为b，此抛物线拱的面积为S，若b=3h，则S等于（　　）

$\frac{3}{2}$h²

$\frac{7}{4}$h²

12．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的短轴长为2，且函数y=x²-$\frac{65}{16}$的图象与椭圆C仅有两个公共点，过原点的直线l与椭圆C交于M，N两点．
（1）求椭圆C的标准方程；
（2）点P为线段MN的中垂线与椭圆C的一个公共点，求△PMN面积的最小值，并求此时直线l的方程．

2．设函数f（x）=$\frac{a}{{x}^{2}}$+lnx，g（x）=x³-x²-3．
（1）函数f（x）在区间[1，+∞）上是单调函数，求实数a的取值范围；
（2）若存在x₁，x₂∈[-$\frac{1}{3}$，3]，使得g（x₁）-g（x₂）≥M成立，求满足条件的最大整数M；
（3）如果对任意的s，t∈[$\frac{1}{3}$，2]都有sf（s）≥g（t）成立，求实数a的范围．

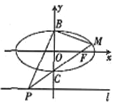如图，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y²=1（a＞1）的长轴长是短轴长的2倍，右焦点为F，点B，C分别是该椭圆的上、下顶点，点P是直线l：y=-2上的一个动点（与y轴交点除外），直线PC交椭圆于另一点M．记直线BM，BP的斜率分别为k₁、k₂
（1）当直线PM过点F时，求$\overrightarrow{PB}•\overrightarrow{PM}$的值；
（2）求|k₁|+|k₂|的最小值．

7．下列函数中，以$\frac{π}{2}$为最小正周期的偶函数是（　　）

$y=cos（{2x+\frac{π}{2}}）$

y=sin²2x-cos²2x