Question

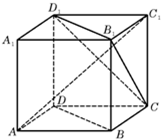ABCD-A₁B₁C₁D₁为正方体，下面结论错误的是

 

①BD∥平面CB₁D₁    
②∠AC₁C=∠AC₁B₁=∠AC₁D₁
③AC₁⊥BD        
④平面CB₁D₁⊥平面AB₁D₁．

Answer 1

分析：①中，判定BD∥平面CB₁D₁正确，②中，判定∠AC₁C=∠AC₁B₁=∠AC₁D₁正确；
③中，判定AC₁⊥BD正确；④中，判定平面CB₁D₁⊥平面AB₁D₁不正确．

解答：解：①中，∵BD∥B₁D₁，BD?平面CB₁D₁，B₁D₁?平面CB₁D₁，∴BD∥平面CB₁D₁正确；    
②中，∵Rt△AC₁C≌Rt△AC₁B₁≌Rt△AC₁D₁，∴∠AC₁C=∠AC₁B₁=∠AC₁D₁正确；
③中，∵BD⊥AC，BD⊥CC₁，且AC∩CC₁=C，∴BD⊥平面ACC₁，∴AC₁⊥BD正确；        
④中，取B₁D₁的中点O₁，连接AO₁，CO₁；则AO₁⊥B₁D₁，CO₁⊥B₁D₁，
∴∠AO₁C是二面角A-B₁D₁-C的平面角；设正方体的棱长为1，则cos∠AO₁C=

( 6 2 )2+( 6 2 )2-( 2 )2

2× 6 2 × 6 2

=

1

3

，
∴∠AO₁C≠90°，∴平面CB₁D₁⊥平面AB₁D₁不正确；
故答案为：④．

点评：本题考查了以正方体为载体的空间中的线面平行、面面垂直等位置关系的判定，是易错题．