题目内容
11.在△ABC中,BC=4,AB=$\sqrt{2}$AC,则△ABC面积的最大值为8$\sqrt{2}$.分析 设AC=x,则AB=$\sqrt{2}$x,根据面积公式得S△ABC=2xsinC,由余弦定理求得 cosC代入化简 S△ABC=$\frac{1}{4}$$\sqrt{2048-({x}^{2}-48)^{2}}$,由三角形三边关系求得4$\sqrt{2}$-4<x<4$\sqrt{2}$+4,由二次函数的性质求得S△ABC取得最大值.
解答 解:设AC=x,则AB=$\sqrt{2}$x,根据面积公式得S△ABC=$\frac{1}{2}$AC•BC•sinC=$\frac{1}{2}$•x•4•sinC=2xsinC,
由余弦定理可得 cosC=$\frac{16-{x}^{2}}{8x}$,
∴S△ABC=2x$\sqrt{1-co{s}^{2}C}$=2x$\sqrt{1-(\frac{16-{x}^{2}}{8x})^{2}}$=$\frac{1}{4}$$\sqrt{2048-({x}^{2}-48)^{2}}$.
由三角形三边关系有:x+$\sqrt{2}$x>4且x+4>$\sqrt{2}$x,解得 4$\sqrt{2}$-4<x<4$\sqrt{2}$+4,
故当 x=4$\sqrt{3}$时,S△ABC取得最大值8$\sqrt{2}$,
故答案为:8$\sqrt{2}$.
点评 本题主要考查了余弦定理和面积公式在解三角形中的应用.当涉及最值问题时,可考虑用函数的单调性和定义域等问题,计算量较大,考查了转化思想,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
7.已知集合A={0,1,2},A∩B={0,2},则B集合可能是( )
| A. | {0,1} | B. | {1,2} | C. | {0,2,3} | D. | {0} |
8.下列命题中正确的是( )
| A. | 若α>β,则sinα>sinβ | |
| B. | 命题:“?x>1,x2>1”的否定是“?x≤1,x2≤1” | |
| C. | 已知函数f(x)=x3+ax2+bx+c,若f(x)在区间(-1,0)上单调递减,则a2+b2的取值范围为$[{\frac{9}{5},+∞})$ | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |
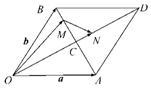 如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,试用a,b表示$\overrightarrow{OM}$,$\overrightarrow{ON}$,$\overrightarrow{MN}$.
如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,试用a,b表示$\overrightarrow{OM}$,$\overrightarrow{ON}$,$\overrightarrow{MN}$.