题目内容
定义
×
=|
||
|sinθ,其中θ为向量
与
的夹角,若|
|=5,|
|=13,
•
=-25,则
×
等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、-60 | B、60 |
| C、-60或60 | D、6 |
考点:数量积表示两个向量的夹角,平面向量数量积的运算
专题:平面向量及应用
分析:由条件利用两个向量的数量积的定义,求出cosθ,结合θ的范围,可得sinθ,从而求得
×
=|
||
|sinθ的值.
| a |
| b |
| a |
| b |
解答:
解:由题意可得5×13×cosθ=-25,cosθ=-
.
再结合θ∈[0,π],∴sinθ=
,
∴
×
=|
||
|sinθ=5×13×
=60,
故选:B.
| 5 |
| 13 |
再结合θ∈[0,π],∴sinθ=
| 12 |
| 13 |
∴
| a |
| b |
| a |
| b |
| 12 |
| 13 |
故选:B.
点评:本题主要考查新定义,两个向量的数量积的定义,属于基础题.

练习册系列答案
相关题目
数列1,4,9,16,25,…的一个通项公式an=( )
| A、n2-1 |
| B、n2 |
| C、2n2-1 |
| D、2n-1 |
下列叙述中正确的是( )
| A、两个数的算术平均数不小于它们的几何平均数 |
| B、两个不等正数的算术平均数大于它们的几何平均数 |
| C、若两个数的和为常数,则它们的积有最大值 |
| D、若两个数的积为常数,则它们的和有最小值 |
函数y=x+
+5(x>1)的最小值为( )
| 1 |
| x-1 |
| A、5 | B、6 | C、7 | D、8 |
“x<0”是“ln(x+1)<0”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充分必要 |
| D、既不充分也不必要 |
三个数0.73.1,0.76,60.7的大小关系为( )
| A、0.73.1<0.76<60.7 |
| B、0.76<0.73.1<60.7 |
| C、0.76<60.7<0.73.1 |
| D、60.7<0.76<0.73.1 |
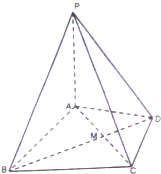 如图,在四棱锥P-ABCD中,PA⊥面ABCD,△ABC是正三角形,AC△与BD的交点M恰好是AC的中点,又是PA=AB=2,∠CDA=120°.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,△ABC是正三角形,AC△与BD的交点M恰好是AC的中点,又是PA=AB=2,∠CDA=120°.