题目内容
若F1,F2分别为双曲线
-
=1的下,上焦点,O为坐标原点,点P在双曲线的下支上,点M在上准线上,且满足
=
,
=λ(
+
)(λ>0),则双曲线的离心率 .
| y2 |
| a2 |
| x2 |
| b2 |
| F2O |
| MP |
| F1M |
| ||
|
|
| ||
|
|
考点:双曲线的简单性质,向量在几何中的应用
专题:圆锥曲线的定义、性质与方程
分析:由题设条件知四边形PF1OM为菱形,且边长为|
|=|
|=c,所以|
|=2a+|
|=2a+c,由此利用椭圆的第二定义能求出椭圆的离心率.
| PF1 |
| F1Q |
| PF2 |
| PF1 |
解答:
解:如图,∵
=
,
=λ(
+
)(λ>0),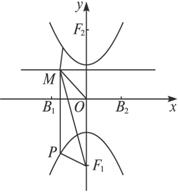
∴
=
,∴PF1OM为平行四边形.且M在∠PF1O的角平分线上,
∴四边形PF1OM为菱形,且边长为|
|=|
|=c,
∴|
|=2a+|
|=2a+c,
由第二定义知
=e,即
=e.
∴
=e,且e>1.
解得e=2.
故答案为:2.
| F2O |
| MP |
| F1M |
| ||
|
|
| ||
|
|

∴
| OF1 |
| MP |
∴四边形PF1OM为菱形,且边长为|
| PF1 |
| F1Q |
∴|
| PF2 |
| PF1 |
由第二定义知
|
| ||
|
|
| 2a+c |
| c |
∴
| 2+e |
| e |
解得e=2.
故答案为:2.
点评:本题考查椭圆的离心率的求法,是中档题,解题时要注意数形结合思想的合理运用.

练习册系列答案
相关题目
等比数列{an}的前n项和为Sn,若a3=6,s3=
4xdx,则公比q的值为( )
| ∫ | 3 0 |
| A、1 | ||
B、-
| ||
C、1或-
| ||
D、-1或-
|