题目内容
10.下列有关命题的叙述,其中错误的个数为( )①若p∨q为真命题,则p∧q也为真命题
②“x>5”是“x2-4x-5>0”的充分不必要条件
③命题:?x∈R,2x>x2的否定为:?x0∉R,2${\;}^{{x}_{0}}$≤x02;
④?x∈R,使得ex=1+x是真命题.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①,若p∨q为真命题,则p、q至少一个为真命题,则p∧q也不一定为真命题;
②,“x>5”⇒“x2-4x-5>0”;“x2-4x-5>0”⇒“x>5或x<-1“;
③,命题:?x∈R,2x>x2的否定为:?x0∈R,2${\;}^{{x}_{0}}$≤x02;
④,当x=0,ex=1+x.
解答 解:对于①,若p∨q为真命题,则p、q至少一个为真命题,则p∧q也不一定为真命题,故错;
对于②,“x>5”⇒“x2-4x-5>0”;“x2-4x-5>0”⇒“x>5或x<-1“,故正确;
对于③,命题:?x∈R,2x>x2的否定为:?x0∈R,2${\;}^{{x}_{0}}$≤x02,故错;
对于④,当x=0,ex=1+x,故正确.
故选:B
点评 本题考查了命题真假的判定,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知集合A={x|y=$\sqrt{2x-{x}^{2}}$},集合B=Z,则A∩B=( )
| A. | {1} | B. | [0,2] | C. | (0,2) | D. | {0,1,2} |
2.已知抛物线C:y2=2px(p>0)的焦点为F,点D(2,y0)在抛物线C上,且|DF|=3,直线y=x-1与抛物线C交于A,B两点,O为坐标原点.
(1)求抛物线C的方程;
(2)求△OAB的面积.
(1)求抛物线C的方程;
(2)求△OAB的面积.
20.《数学统综》有如下记载:“有凹线,取三数,小小大,存三角”.意思是说“在凹(或凸)函数(函数值为正)图象上取三个点,如果在这三点的纵坐标中两个较小数之和大于最大的数,则存在将这三点的纵坐标值作为三边长的三角形”.现已知凹函数f(x)=x2-2x+2,在$[\frac{1}{3},{m^2}-m+2]$上任取三个不同的点(a,f(a)),(b,f(b)),(c,f(c)),均存在以f(a),f(b),f(c)为三边长的三角形,则实数m的取值范围为( )
| A. | [0,1] | B. | $[0,\frac{{\sqrt{2}}}{2})$ | C. | $(0,\frac{{\sqrt{2}}}{2}]$ | D. | $[\frac{{\sqrt{2}}}{2},\sqrt{2}]$ |
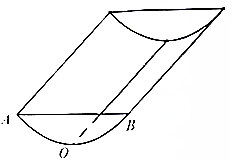 某小区内有一条形状如图的沟渠,沟沿是两条平行线段,沟渠宽AB为20厘米,沟渠的直截面ABO为一段抛物线,抛物线顶点为O,对称轴与地面垂直,沟渠深20厘米,沟渠中水深10厘米.
某小区内有一条形状如图的沟渠,沟沿是两条平行线段,沟渠宽AB为20厘米,沟渠的直截面ABO为一段抛物线,抛物线顶点为O,对称轴与地面垂直,沟渠深20厘米,沟渠中水深10厘米.