题目内容

20．设随机变量ξ的分布列为P（ξ=k）=$\frac{1}{5}$（k=1，2，3，4，5），求：（1）E（ξ+2）2；（2）D（2ξ-1）．

分析 （1）先求出E（ξ），再求出D（ξ），然后由E（ξ2）=D（ξ）+E2（ξ），E（ξ+2）2=E（ξ2+4ξ+4）=E（ξ2）+4E（ξ）+4，能求出结果．
=11+12+4=27．
（2）由D（2ξ-1）=4D（ξ），能求出结果．

解答 解：（1）∵随机变量ξ的分布列为P（ξ=k）=$\frac{1}{5}$（k=1，2，3，4，5），
∴E（ξ）=$\frac{1}{5}$（1+2+3+4+5）=3，
D（ξ）=$\frac{1}{5}$[（1-3）2+（2-3）2+（3-3）2+（4-3）2+（5-3）2]=2，
∴E（ξ2）=D（ξ）+E2（ξ）=2+9=11，
∴E（ξ+2）2=E（ξ2+4ξ+4）=E（ξ2）+4E（ξ）+4
=11+12+4=27．
（2）D（2ξ-1）=4D（ξ）=8．

点评 本题考查离散型随机变量的数学期望和方差，是基础题，解题时要认真审题，注意数学期望和方差的性质的合理运用．

练习册系列答案
相关题目
10．（1）已知y=f（x）是定义在R的奇函数，且在R上为增函数．求不等式f（4x-5）＞0的解集；
（2）已知偶函数f（x）（x∈R），当x≥0时．f（x）=x（5-x）+1，求f（x）在R上的解析式．
11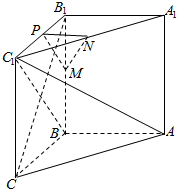．如图所示，在直三棱柱ABC-A1B1C1中，∠ABC=90°，BC=CC1，M、N、P分别是BB1、A1C1、B1C1的中点．
（1）求证：CB1⊥平面ABC1；
（2）求证：面MNP∥面ABC1．
8．不求值，比较下列各对三角函数值的大小：
（1）cos（-$\frac{π}{7}$），cos（-$\frac{π}{3}$）；
（2）sin$\frac{4π}{5}$，sin$\frac{2π}{7}$；
（3）cos$\frac{2π}{5}$，sin$\frac{2π}{5}$．
15．已知数列{an}的各项都为自然数，前n项和为Sn，且存在整数λ，使得对任意正整数n都有Sn=（1+λ）an-λ恒成立．
（1）求λ值，使得数列{an}为等差数列，并求数列{an}的通项公式；
（2）若数列{an}为等比数列，此时存在正整数k，当1≤k＜j时，有$\underset{\stackrel{i}{∑}}{i=k}$ai=2016，求k．
5．△ABC的顶点坐标是A（3，1，1），B（-5，2，1），C（-$\frac{8}{3}$，2，3），则它在yOz平面上射影图形的面积是（　　）
A．4B．3C．2D．1
12．已知函数f（x）=sinωx-$\sqrt{3}$cosωx（ω＞0）的图象的相邻两对称轴间的距离为$\frac{π}{2}$，则当x∈[-$\frac{π}{2}$，0]时，f（x）的最大值和单调增区间分别为（　　）
A．1，[-$\frac{π}{2}$，-$\frac{π}{6}$]B．1，[-$\frac{π}{2}$，-$\frac{π}{12}$]C．$\sqrt{3}$，[-$\frac{π}{6}$，0]D．$\sqrt{3}$，[-$\frac{π}{12}$，0]
10．△ABC的三个内角A，B，C，若$\frac{\sqrt{3}cosA+sinA}{\sqrt{3}sinA-cosA}$=tan（-$\frac{7}{12}$π），则2cosB+sin2C的最大值为$\frac{3}{2}$．
11．若xlog52≥-1，则函数f（x）=4x-2x+1-3的最小值为（　　）
A．-4B．-3C．-1D．0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网