题目内容
9.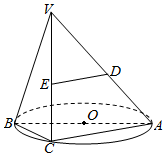 如图,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D、E分别是VA、VC的中点.
如图,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D、E分别是VA、VC的中点.(1)若F∈BC试确定点F的位置,使VB∥平面EDF,并证明;
(2)证明:VB⊥DE.
分析 (1)点F为BC的中点时,VB∥平面EDF,利用线线平行,即可得出线面平行;
(2)利用直径对直角,得出AC⊥BC,再由直线VC⊥AC,证明AC⊥平面VBC,再由ED∥AC,得出ED⊥平面VBC,从而证明VB⊥DE.
解答 解:(1)如图所示,
当点F为BC的中点时,VB∥平面EDF,
∵F为BC的中点,∴E为VC的中点,
∴EF∥VB,
又EF?平面DEF,VB?平面DEF,
∴VB∥平面EDF;
(2)∵AB是⊙O的直径,点C是⊙O上的点,
∴AC⊥BC,
又直线VC垂直于⊙O所在的平面,
∴VC⊥AC,
又VC∩BC=C,∴AC⊥平面VBC;
又D、E分别是VA、VC的中点,
∴ED∥AC,
∴ED⊥平面VBC,
又VB?平面VBC,
∴VB⊥DE.
点评 本题考查了空间中的平行与垂直共线的应用问题,也考查了逻辑思维与空间想象能力,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知集合P={0,1},Q={0},则( )
| A. | Q=∅ | B. | P=Q | C. | P?Q | D. | P⊆Q |
4.已知f(x)是定义在R上的偶函数,且在(-∞,0)上单调递增,a=f(0.80.8),b=f(0.81.6),c=f(1.60.8),则a,b,c的大小关系是( )
| A. | c<a<b | B. | a<c<b | C. | a<b<c | D. | c<b<a |
18.设函数f(x)=|2x-1|,c<b<a,且f(c)>f(a)>f(b),则2a+2c与2的大小关系是( )
| A. | 2a+2c>2 | B. | 2a+2c≥2 | C. | 2a+2c≤2 | D. | 2a+2c<2 |
 某次运动会甲、乙两名射击运动员的成绩如下:
某次运动会甲、乙两名射击运动员的成绩如下: