题目内容
17.已知函数f(x)=$\frac{1}{3}$x3-2ax2+3a2x+b(a>0).(1)当y=f(x)的极小值为1时,求b的值;
(2)若f(x)在区间[1,2]上是减函数,求a的范围.
分析 (1)求出函数的导数,得到函数的单调区间,从而求出f(3a)是函数的极小值,求出b的值即可;
(2)根据函数的单调性得到[1,2]⊆[a,3a],求出a的范围化简.
解答 解:(1)f′(x)=x2-4ax+3a2=(x-a)(x-3a),
令f′(x)≥0,解得:x≤a,x≥3a,
令f′(x)<0,解得:a<x<3a,
故f(x)在(-∞,a)递增,在(a,3a)递减,在(3a,+∞)递增,
由函数的单调性可知,函数在x=3a处取极小值,
即f(3a)=$\frac{1}{3}$(3a)3-2a(3a)2+3a23a+b=1,
所以b=1;
(2)f′(x)=x2-4ax+3a2=(x-a)(x-3a),
要使f(x)在区间[1,2]上是减函数,
则导数在[1,2]小于等于0,
即[1,2]⊆[a,3a],
故$\left\{\begin{array}{l}{3a≥2}\\{a≤1}\end{array}\right.$,
所以$\frac{2}{3}$≤a≤1.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及集合的包含关系,是一道中档题.

练习册系列答案
相关题目
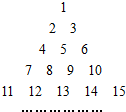 将全体正整数排成一个三角形数阵:按照如图所示排列的规律:
将全体正整数排成一个三角形数阵:按照如图所示排列的规律: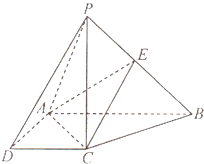 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,AB∥DC,∠ADC=90°,PC=AB=2AD=2DC=2,点E为PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,AB∥DC,∠ADC=90°,PC=AB=2AD=2DC=2,点E为PB的中点. .
. 的极值;
的极值; ,当
,当 时,
时, 在区间
在区间 内存在极值,求整数
内存在极值,求整数 的值.
的值.