题目内容
15．已知f（n）=$\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+…+$\frac{1}{3n+1}$，则f（k+1）等于（ ）| A． | f（k）+$\frac{1}{3（k+1）+1}$ | B． | f（k）+$\frac{2}{3k+2}$ | ||
| C． | f（k）+$\frac{1}{3k+2}$+$\frac{1}{3k+3}$+$\frac{1}{3k+4}$-$\frac{1}{k+1}$ | D． | f（k）+$\frac{1}{3k+4}$-$\frac{1}{k+1}$ |
分析 根据f（n）的解析式分别写出f（k）与f（k+1），即可得出结论．
解答 解：f（n）=$\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+…+$\frac{1}{3n+1}$，
∴f（k）=$\frac{1}{k+1}$+$\frac{1}{k+2}$+$\frac{1}{k+3}$+…+$\frac{1}{3k+1}$
f（k+1）=$\frac{1}{（k+1）+1}$+$\frac{1}{（k+1）+2}$+$\frac{1}{（k+1）+3}$+…+$\frac{1}{3（k+1）+1}$
=$\frac{1}{k+2}$+$\frac{1}{k+3}$+$\frac{1}{k+4}$+…+$\frac{1}{3k+4}$
=f（k）+$\frac{1}{3k+2}$+$\frac{1}{3k+3}$+$\frac{1}{3k+4}$-$\frac{1}{k+1}$．
故选：C．
点评 本题考查了根据函数解析式写出对应函数值的应用问题，是基础题目．
练习册系列答案
相关题目
5．设函数f（x）=x3-4x-a，0＜a＜2．若f（x）的三个零点为x1，x2，x3，且x1＜x2＜x3，则（ ）
| A． | x1＜-2 | B． | x2＞0 | C． | x3＜1 | D． | x3＞2 |
3．已知函数f（x）=ax3+bx2+cx，其导函数为f′（x）的部分值如表所示：
根据表中数据，回答下列问题：
（Ⅰ）实数c的值为6；当x=3时，f（x）取得极大值（将答案填写在横线上）．
（Ⅱ）求实数a，b的值．
（Ⅲ）求f（x）的单调区间．
| x | -2 | 0 | 1 | 3 | 8 |
| f′（x） | -10 | 6 | 8 | 0 | -90 |
（Ⅰ）实数c的值为6；当x=3时，f（x）取得极大值（将答案填写在横线上）．
（Ⅱ）求实数a，b的值．
（Ⅲ）求f（x）的单调区间．
10．已知函数f（x）=（3-a）x-2+a-2lnx（a∈R）．
（Ⅰ）若a≤3，试讨论函数f（x）的单调性；
（Ⅱ）若函数f（x）＞x在（0，$\frac{1}{2}$）上恒成立，求实数a的取值范围．
（Ⅰ）若a≤3，试讨论函数f（x）的单调性；
（Ⅱ）若函数f（x）＞x在（0，$\frac{1}{2}$）上恒成立，求实数a的取值范围．
20．设f（x）与g（x）是定义在同一区间[a，b]上的两个函数，若函数y=f（x）-g（x）在[a，b]上两个不同的零点，则称f（x）与g（x）的“关联区间”，若f（x）=$\frac{1}{3}{x^3}-{x^2}$-x与g（x）=2x+b的“关联区间”是[-3，0]，则b的取值范围是（ ）
| A． | [-9，0] | B． | $[0，\frac{5}{3}]$ | C． | $[-9，\frac{5}{3}]$ | D． | $[0，\frac{5}{3}）$ |
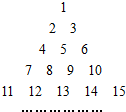将全体正整数排成一个三角形数阵：按照如图所示排列的规律：