题目内容
12．已知函数f（x）=asinx在点（0，0）处的切线方程为y=2x，则a=（ ）| A． | 1 | B． | 2 | C． | 4 | D． | $\frac{1}{2}$ |
分析 由题意求导y′=acosx，从而可得acos0=2；从而解得a的值．
解答 解：函数f（x）=asinx的导数为y′=acosx，
∵函数f（x）=asinx在点（0，0）处的切线方程为y=2x，
而y=2x的斜率为2，
故acos0=2，
解得，a=2．
故选：B．
点评 本题考查了导数的求法及其几何意义的应用，属于基础题．
练习册系列答案
挑战100单元检测试卷系列答案
名题金卷系列答案
相关题目
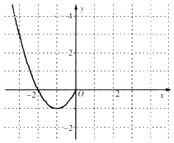已知函数f（x）是定义在R上的偶函数，且当x≤0时，f（x）=x2+2x．
某教育主管部门到一所中学检查学生的体质健康情况．从全体学生中，随机抽取12名进行体质健康测试，测试成绩（百分制）以茎叶图形式表示如图：