题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}x+2,x>a\\ x{\;}^{2}+5x+2,x≤a\end{array}$函数g(x)=f(x)-2x恰有2个不同的零点,则实数a 的取值范围是[2,+∞).分析 化简g(x)=f(x)-2x,而方程-x+2=0的解为2,方程x2+3x+2=0的解为-1,-2;推出a的不等式组,从而可得答案.
解答  解:∵f(x)=$\left\{\begin{array}{l}x+2,x>a\\ x{\;}^{2}+5x+2,x≤a\end{array}$,
解:∵f(x)=$\left\{\begin{array}{l}x+2,x>a\\ x{\;}^{2}+5x+2,x≤a\end{array}$,
∴g(x)=f(x)-2x=$\left\{\begin{array}{l}{-x+2,x>a}\\{{x}^{2}+3x+2,x≤a}\end{array}\right.$,
而方程-x+2=0的解为2,方程x2+3x+2=0的解为-1,-2;
若函数g(x)=f(x)-2x恰有2个不同的零点,
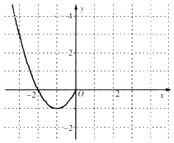
a<2时,由函数的图象可知:函数的零点有3个,当a∈[2,+∞)时,函数的零点有2个.
即实数a的取值范围是:[2,+∞).
故答案为:[2,+∞)
点评 本题考查了分段函数的化简与函数零点的判断,属于中档题.

练习册系列答案
相关题目
16.下列关系中,属于相关关系的是( )
| A. | 正方形的边长与面积 | B. | 农作物的产量与施肥量 | ||
| C. | 人的身高与眼睛近视的度数 | D. | 哥哥的数学成绩与弟弟的数学成绩 |
 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.