题目内容
设直线
ax+by=1(其中a,b为实数)与圆x2+y2=1相交于A,B两点,△AOB是直角三角形(O为坐标原点),则点P(a,b)到点M(0,1)的距离的最大值为$( )
| 2 |
A、
| ||
| B、2 | ||
C、2
| ||
D、
|
考点:直线与圆的位置关系
专题:综合题,直线与圆,圆锥曲线的定义、性质与方程
分析:根据圆的方程找出圆心坐标和半径,由|OA|=|OB|根据题意可知△AOB是等腰直角三角形,根据勾股定理求出|AB|的长度,根据等腰直角三角形的性质可得圆心到直线的距离等于|AB|的一半,然后利用点到直线的距离公式表示出圆心到直线的距离,两者相等即可得到a与b的轨迹方程为一个椭圆,由图形可知点P(a,b)到焦点(0,1)的距离的最大值.
解答:
 解:由圆x2+y2=1,所以圆心(0,0),半径为1
解:由圆x2+y2=1,所以圆心(0,0),半径为1
所以|OA|=|OB|=1,则△AOB是等腰直角三角形,得到|AB|=
,
则圆心(0,0)到直线
ax+by=1的距离为
=
,
∴2a2+b2=2,即a2+
=1.
因此所求距离为椭圆a2+
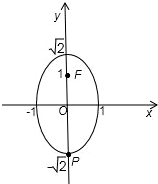
=1上点P(a,b)到焦点(0,1)的距离,
如图得到其最大值PF=
+1
故选A
 解:由圆x2+y2=1,所以圆心(0,0),半径为1
解:由圆x2+y2=1,所以圆心(0,0),半径为1所以|OA|=|OB|=1,则△AOB是等腰直角三角形,得到|AB|=
| 2 |
则圆心(0,0)到直线
| 2 |
| 1 | ||
|
| ||
| 2 |
∴2a2+b2=2,即a2+
| b2 |
| 2 |
因此所求距离为椭圆a2+
| b2 |
| 2 |
如图得到其最大值PF=
| 2 |
故选A
点评:此题考查学生灵活点到直线的距离公式化简求值,综合运用所学的知识求动点形成的轨迹方程,是一道综合题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
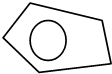 如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置的可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为( )
如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置的可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为( )| A、4π | B、5π | C、6π | D、7π |