题目内容
设集合I={0,1,2,3,4,5}.选择I的两个非空子集A和B,要使B中最小的数大于A中最大的数,则不同的选择方法共有( )
| A、49种 | B、50种 |
| C、129种 | D、130种 |
考点:排列、组合及简单计数问题
专题:应用题,排列组合
分析:根据题意,B中最小的数大于A中最大的数,则集合A、B中没有相同的元素,且都不是空集,按A、B中元素数目这和的情况,分5种情况讨论,分别计算其选法种数,进而相加可得答案.
解答:
解:集合A、B中没有相同的元素,且都不是空集,
从6个元素中选出2个元素,有C62=15种选法,小的给A集合,大的给B集合;
从6个元素中选出3个元素,有C63=20种选法,再分成1一个元素一组、2个元素一组,有两种分法,较小元素的一组给A集合,较大元素的一组的给B集合,共有2×20=40种方法;
从6个元素中选出4个元素,有C64=15种选法,再分成1个元素一组、3三个元素一组;2个元素一组、2个元素一组;3个元素一组、1一个元素一组,共三种分法,较小元素的一组给A集合,较大元素的一组的给B集合,共有3×15=45种方法;
从6个元素中选出5个元素,有C65=6种选法,再分成1个元素一组、4个元素一组;2个元素一组、3个元素一组;3个元素一组、2个元素一组;4个元素一组、1两个元素一组,有四种分法,较小元素的一组给A集合,较大元素的一组的给B集合,共有6×4=24种方法;
从6个元素中选出6个元素,有C66=1种选法,再分成1个元素一组、5个元素一组;2个元素一组、4个元素一组;3个元素一组、3个元素一组;4个元素一组、2个元素一组;5个元素一组、1两个元素一组,有五种分法,较小元素的一组给A集合,较大元素的一组的给B集合,共有5种方法;
总计为15+40+45+24+5=129种方法.
故选:C.
从6个元素中选出2个元素,有C62=15种选法,小的给A集合,大的给B集合;
从6个元素中选出3个元素,有C63=20种选法,再分成1一个元素一组、2个元素一组,有两种分法,较小元素的一组给A集合,较大元素的一组的给B集合,共有2×20=40种方法;
从6个元素中选出4个元素,有C64=15种选法,再分成1个元素一组、3三个元素一组;2个元素一组、2个元素一组;3个元素一组、1一个元素一组,共三种分法,较小元素的一组给A集合,较大元素的一组的给B集合,共有3×15=45种方法;
从6个元素中选出5个元素,有C65=6种选法,再分成1个元素一组、4个元素一组;2个元素一组、3个元素一组;3个元素一组、2个元素一组;4个元素一组、1两个元素一组,有四种分法,较小元素的一组给A集合,较大元素的一组的给B集合,共有6×4=24种方法;
从6个元素中选出6个元素,有C66=1种选法,再分成1个元素一组、5个元素一组;2个元素一组、4个元素一组;3个元素一组、3个元素一组;4个元素一组、2个元素一组;5个元素一组、1两个元素一组,有五种分法,较小元素的一组给A集合,较大元素的一组的给B集合,共有5种方法;
总计为15+40+45+24+5=129种方法.
故选:C.
点评:本题考查排列组合的实际应用,本题解题的关键是理解题意,能够看懂使B中的最小数大于A中的最大数的意义,本题是一个难题也是一个易错题,需要认真解答.

练习册系列答案
相关题目
若a>1则a-1+
的最小值等于( )
| 1 |
| a-1 |
| A、a | ||||
B、
| ||||
| C、2 | ||||
| D、3 |
x=
(n>3),则x是( )
| n! |
| 3! |
A、C
| ||
B、C
| ||
C、A
| ||
D、A
|
已知函数y=f(x)在x=x0处可导,则
等于( )
| lim |
| h→0 |
| f(x0)-f(x0-h) |
| h |
| A、f′(x0) |
| B、2f′(x0) |
| C、-2f′(x0) |
| D、0 |
方程x3-x-1=0仅有一个正实数解x,则x∈( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
在△ABC中,角A、B、C的对边分别为a、b、c,则acosB+bcosA等于( )
A、
| ||
| B、b | ||
| C、c | ||
| D、a |
如图是导函数y=f′(x)的图象,那么函数y=f(x)在区间[a,b]内的极值点有( )
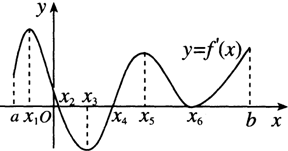

| A、0 | B、1 | C、2 | D、3 |
 已知函数f(x)=
已知函数f(x)=