题目内容
已知复数z=1+2i,则
=( )
| 1 |
| z |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用分子分母分别乘以分母的共轭复数将分母实数化解答.
解答:
解:∵z=1+2i,
=
=
=
=
-
i;
故选:C.
| 1 |
| z |
| 1 |
| 1+2i |
| 1-2i |
| (1+2i)(1-2i) |
| 1-2i |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
故选:C.
点评:本题考查了复数的除法运算,只要分子分母分别乘以分母的共轭复数,将分母实数化.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
已知f(x)=x(2012+lnx),若f′(x0)=2013,则x0=( )
| A、e2 | B、1 |
| C、ln2 | D、e |
x=
(n>3),则x是( )
| n! |
| 3! |
A、C
| ||
B、C
| ||
C、A
| ||
D、A
|
从(
+
)20的展开式中任取一项,则取到有理项的概率为( )
| 4 | x |
| 1 | ||
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数y=f(x)在x=x0处可导,则
等于( )
| lim |
| h→0 |
| f(x0)-f(x0-h) |
| h |
| A、f′(x0) |
| B、2f′(x0) |
| C、-2f′(x0) |
| D、0 |
方程x3-x-1=0仅有一个正实数解x,则x∈( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
如图是导函数y=f′(x)的图象,那么函数y=f(x)在区间[a,b]内的极值点有( )
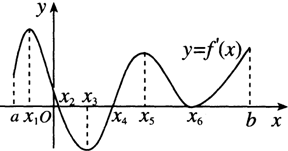

| A、0 | B、1 | C、2 | D、3 |
