题目内容
6.已知函数f(x)=kx-2,f(1)=-1,则f(2)=( )| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
分析 根据f(1)=-1得到k-2=-1,解得k=1,求得函数解析式f(x)=x-2,因而f(2)=0.
解答 解:因为f(x)=kx-2,
且f(1)=-1,所以k-2=-1,
解得k=1,所以,f(x)=k-2,
因此,f(2)=0,
故答案为:A.
点评 本题主要考查了函数值的求解,以及函数解析式的确定,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.若∠A=22°,∠B=23°,则(1+tanA)(1+tanB)的值是( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 1+$\sqrt{2}$ | D. | 2(tanA+tanB) |
11.已知数列{an}为等差数列,且a2=4,a6=12,则公差d=( )
| A. | 6 | B. | 3 | C. | 8 | D. | 2 |
1.某几何体的一条棱长为3,在该几何体的正视图中,这条棱的投影长为2的线段,在该几何体的侧视图和俯视图中,这条棱长的投影长分别是a和b的线段,则a+b的最大值为( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{7}$ | C. | 4 | D. | 2$\sqrt{6}$ |
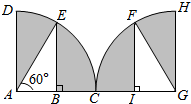 如图所示,两个四分之一圆面ACD和GCH交于点C点,AD=CH=10厘米,∠EAB=∠FGC=60°,EB与FI分别垂直于AC和GC,则阴影部分为85.28平方厘米.(π取3.14)
如图所示,两个四分之一圆面ACD和GCH交于点C点,AD=CH=10厘米,∠EAB=∠FGC=60°,EB与FI分别垂直于AC和GC,则阴影部分为85.28平方厘米.(π取3.14)