题目内容
18．若函数y=x2-3x-4的定义域为[0，m]，值域为[-$\frac{25}{4}$，-4]，则m的最大值是3．分析 根据函数的函数值f（$\frac{3}{2}$）=-$\frac{25}{4}$，f（0）=-4，结合函数的图象即可求解
解答 解：∵f（x）=x2-3x-4=（x-$\frac{3}{2}$）2-$\frac{25}{4}$，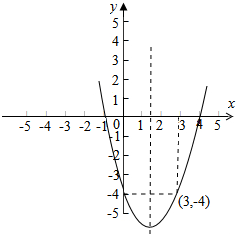
∴f（$\frac{3}{2}$）=-$\frac{25}{4}$，又f（0）=-4，
故由二次函数图象可知：
m的值最小为$\frac{3}{2}$；最大为3．
故答案为3．
点评 本题考查了二次函数的性质，特别是利用抛物线的对称特点进行解题，属于基础题．
练习册系列答案
相关题目
7．数列4，a，9是等比数列是“a=±6”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
8．$\frac{5i}{2-i}$=（ ）
| A． | 1+2i | B． | -1+2i | C． | -1-2i | D． | 1-2i |
6．函数f（x）=3sin（x+$\frac{π}{6}$）在x=θ时取得最大值，则tanθ等于（ ）
| A． | -$\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | -$\sqrt{3}$ | D． | $\sqrt{3}$ |
3．已知集合A={-3，-2，-1，0，1，2}，B={x|-2≤x＜3}，则A∩B=（ ）
| A． | {-2，-1，0} | B． | {-2，-1，0，1} | C． | {-2，-1，0，1，2} | D． | {-2，-1，0，1，2，3} |
10．直线x+y-2=0与坐标轴围成的三角形的面积为（ ）
| A． | 1 | B． | 2 | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
已知函数$y=\frac{1}{|2x|-1}$，求：