题目内容
20.某产品的广告费用x与销售额y的统计数据如表| 广 告 费 用x (万元) | 4 | 2 | 3 | 5 |
| 销 售 额y (万元) | 49 | 26 | a | 54 |
| A. | 37 | B. | 38 | C. | 39 | D. | 40 |
分析 求出数据中心($\overline{x}$,$\overline{y}$),代入回归方程解出a.
解答 解:$\overline{x}$=$\frac{4+2+3+5}{4}$=3.5,$\overline{y}$=$\frac{49+26+a+54}{4}$=$\frac{129+a}{4}$.
∴$\frac{129+a}{4}$=8×3.5+14,解得a=39.
故选:C.
点评 本题考查了线性回归方程的特点,属于基础题.

练习册系列答案
相关题目
10.已知角α的终边上一点P的坐标为(sin$\frac{2π}{3}$,cos$\frac{2π}{3}$),则角α的最小正角为( )
| A. | $\frac{5π}{3}$ | B. | $\frac{2}{3}$π | C. | $\frac{5}{6}$π | D. | $\frac{11}{6}$π |
8.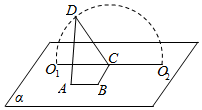 如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )
如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )
 如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )
如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )| A. | 一直变小 | B. | 一直变大 | ||
| C. | 先变小,后变大 | D. | 先变小,再变大,后变小 |
10.下列函数,在其定义域内,既是减函数又是奇函数的是( )
| A. | $y={({\frac{1}{2}})^x}$ | B. | $y={2^{{{log}_2}x}}$ | C. | y=2x | D. | $y={log_2}{2^{-x}}$ |
 任取实数x∈[2,30],执行如图所示的程序框图,则输出的x不小于79的概率是$\frac{3}{4}$.
任取实数x∈[2,30],执行如图所示的程序框图,则输出的x不小于79的概率是$\frac{3}{4}$.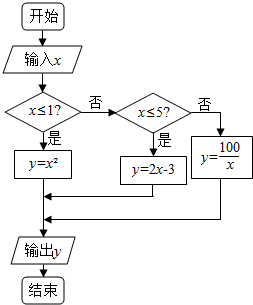 如图,给出了一个程序框图,其作用是输入x的值,输出相应y的值.
如图,给出了一个程序框图,其作用是输入x的值,输出相应y的值.