题目内容
已知数列{an}的前n项和为Sn,且Sn=4an-3(n∈N*).
(1)证明:数列{an}是等比数列;
(2)若数列{bn}满足bn+1=an+bn(n∈N*),且b1=2,求数列{bn}的通项公式.
(1)证明:因为Sn=4an-3,所以n=1时,a1=4a1-3,解得a1=1.
因为Sn=4an-3,则Sn-1=4an-1-3(n≥2),
所以当n≥2时,an=Sn-Sn-1=4an-4an-1,
整理得an=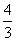 an-1.
an-1.
又a1=1≠0,
所以{an}是首项为1,公比为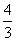 的等比数列.
的等比数列.
(2)因为an=(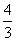 )n-1,bn+1=an+bn(n∈N*),
)n-1,bn+1=an+bn(n∈N*),
所以bn+1-bn=(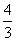 )n-1.
)n-1.
可得bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)
=2+
=3·(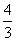 )n-1-1(n≥2),
)n-1-1(n≥2),
当n=1时也符合上式,∴bn=3·(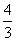 )n-1-1.
)n-1-1.

练习册系列答案
相关题目
在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的3,5,8,13,22,39,…,为数列{bn},则
| 第1行 | 1 | 2 | 4 | 8 | … |
| 第2行 | 2 | 3 | 5 | 9 | … |
| 第3行 | 3 | 5 | 8 | 13 | … |
| …… |
(1)此数表中的第2行第8列的数为________;
(2)数列{bn}的通项公式为________.
 ,一个等比中项是
,一个等比中项是 ,且a>b,则双曲线
,且a>b,则双曲线 -
- =1的离心率e等于( )
=1的离心率e等于( ) B.
B. C.
C. D.
D.
 B.5 C.-
B.5 C.-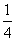 )>lgx(x>0)
)>lgx(x>0)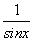 ≥2(x≠kπ,k∈Z)
≥2(x≠kπ,k∈Z)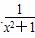 >1(x∈R)
>1(x∈R)