题目内容
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义f″(x)是y=f(x)的导函数y=f′(x)的导函数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数f(x)=ax3+bx2+cx+d(a≠0)都关于点(-
,f(-
))对称:
②存在三次函数有两个及两个以上的对称中心;
③存在三次函数f(x)=ax3+bx2+cx+d(a≠0),若f′(x)=0有实数解x0,则点(x0,f(x0))为函数y=f(x)的对称中心;
④若函数g(x)=
x3-
x2-
,则:g(
)+g(
)+g(
)+…+g(
)=-1006.5
其中所有正确结论的序号是( )
①任意三次函数f(x)=ax3+bx2+cx+d(a≠0)都关于点(-
| b |
| 3a |
| b |
| 3a |
②存在三次函数有两个及两个以上的对称中心;
③存在三次函数f(x)=ax3+bx2+cx+d(a≠0),若f′(x)=0有实数解x0,则点(x0,f(x0))为函数y=f(x)的对称中心;
④若函数g(x)=
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2014 |
| 2 |
| 2014 |
| 3 |
| 2014 |
| 2013 |
| 2014 |
其中所有正确结论的序号是( )
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
考点:导数的运算
专题:导数的概念及应用
分析:①根据函数f(x)的解析式求出f′(x)和f″(x),令f″(x)=0,求得x的值,
由此求得三次函数f(x)=ax3+bx2+cx+d(a≠0)的对称中心;
②③利用三次函数对称中心的定义和性质进行判断;
④函数g(x)=
x3-
x2-
的对称中心是(
,-
),得g(x)+(g(1-x)=-1,由此求得g(
)+g(
)+g(
)+…+g(
)=-1006.5
由此求得三次函数f(x)=ax3+bx2+cx+d(a≠0)的对称中心;
②③利用三次函数对称中心的定义和性质进行判断;
④函数g(x)=
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2014 |
| 2 |
| 2014 |
| 3 |
| 2014 |
| 2013 |
| 2014 |
解答:
解:∵f(x)=ax3+bx2+cx+d(a≠0),
∴f′(x)=3ax2+2bx+c,f''(x)=6ax+2b,
∵f″(x)=6a×(-
)+2b=0
∴任意三次函数f(x)=ax3+bx2+cx+d(a≠0)都关于点(-
,f(-
))对称:即①正确;
∵任何三次函数都有对称中心,且“拐点”就是对称中心,
∴存在三次函数f′(x)=0有实数解x0,点(x0,f(x0))为y=f(x)的对称中心,即③正确;
任何三次函数都有且只有一个对称中心,故②不正确;
∵函数g(x)=
x3-
x2-
,
∴g′(x)=x2-x,g''(x)=2x-1,
令g''(x)=2x-1=0,得x=
,
∵g(
)=
×(
)3-
×(
)2-
=-
,
∴函数g(x)=
x3-
x2-
的对称中心是(
,-
)
∴g(
)+g(
)+g(
)+…+g(
)=-1006.5,故④正确.
故正确结论为:①③④.
故选:C
∴f′(x)=3ax2+2bx+c,f''(x)=6ax+2b,
∵f″(x)=6a×(-
| b |
| 3a |
∴任意三次函数f(x)=ax3+bx2+cx+d(a≠0)都关于点(-
| b |
| 3a |
| b |
| 3a |
∵任何三次函数都有对称中心,且“拐点”就是对称中心,
∴存在三次函数f′(x)=0有实数解x0,点(x0,f(x0))为y=f(x)的对称中心,即③正确;
任何三次函数都有且只有一个对称中心,故②不正确;
∵函数g(x)=
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
∴g′(x)=x2-x,g''(x)=2x-1,
令g''(x)=2x-1=0,得x=
| 1 |
| 2 |
∵g(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2 |
∴函数g(x)=
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
∴g(
| 1 |
| 2014 |
| 2 |
| 2014 |
| 3 |
| 2014 |
| 2013 |
| 2014 |
故正确结论为:①③④.
故选:C
点评:本小题主要考查函数与导数等知识,考查化归与转化的数学思想方法,考查化简计算能力,求函数的值以及函数的对称性的应用,属于难题.

练习册系列答案
相关题目
给定函数y=f(x)的图象如下列图中,经过原点和(1,1),且对任意an∈(0,1),由关系式an+1=f(an)得到数列{an},满足an+1>an(n∈N*),则该函数的图象为( )
A、 |
B、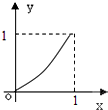 |
C、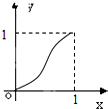 |
D、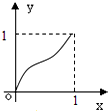 |
观察如图数表规律,可得从数2013到2014的箭头方向是( )

A、 |
B、 |
C、 |
D、 |
函数f(x)=x2•cosx在区间[-
,
]内的图象大致为( )
| π |
| 2 |
| π |
| 2 |
A、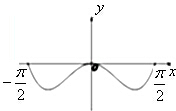 |
B、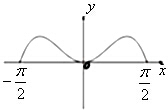 |
C、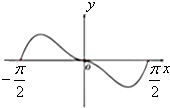 |
D、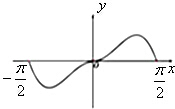 |
设ξ为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,ξ=0;当两条棱平行时,ξ的值为两条棱之间的距离;当两条棱异面时,ξ=1.则P(ξ=0)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)在x0处可导,则
等于( )
| lim |
| △x→0 |
| f(x0-2h)-f(x0) |
| h |
| A、2f′(x0) |
| B、-f′(-x0) |
| C、-f′(x0) |
| D、-2f′(x0) |
设点A,B分别在直线3x-y+5=0和3x-y-13=0上运动,线段AB的中点M恒在圆x2+y2=8内,则点M的横坐标的取值范围为( )
A、(
| ||
B、(-2,-
| ||
C、(2,
| ||
D、(-
|