题目内容
8.若正数x,y满足15x-y=22,则x3+y3-x2-y2的最小值为1.分析 由题意可得x>$\frac{22}{15}$,y>0,又x3+y3-x2-y2=(x3-x2)+(y3-y2),求出y3-y2≥-$\frac{1}{4}$y,当且仅当y=$\frac{1}{2}$时取得等号,设f(x)=x3-x2,求出导数和单调区间、极值和最值,即可得到所求最小值.
解答 解:由正数x,y满足15x-y=22,可得y=15x-22>0,则x>$\frac{22}{15}$,y>0,
又x3+y3-x2-y2=(x3-x2)+(y3-y2),
其中y3-y2+$\frac{1}{4}$y=y(y2-y+$\frac{1}{4}$)=y(y-$\frac{1}{2}$)2≥0,
即y3-y2≥-$\frac{1}{4}$y,
当且仅当y=$\frac{1}{2}$时取得等号,
设f(x)=x3-x2,f(x)的导数为f′(x)=3x2-2x=x(3x-2),
当x=$\frac{3}{2}$时,f(x)的导数为$\frac{3}{2}$×($\frac{9}{2}$-2)=$\frac{15}{4}$,
可得f(x)在x=$\frac{3}{2}$处的切线方程为y=$\frac{15}{4}$x-$\frac{9}{2}$.
由x3-x2≥$\frac{15}{4}$x-$\frac{9}{2}$?(x-$\frac{3}{2}$)2(x+2)≥0,
当x=$\frac{3}{2}$时,取得等号.
则x3+y3-x2-y2=(x3-x2)+(y3-y2)≥$\frac{15}{4}$x-$\frac{9}{2}$-$\frac{1}{4}$y≥$\frac{9}{8}$-$\frac{1}{8}$=1.
当且仅当x=$\frac{3}{2}$,y=$\frac{1}{2}$时,取得最小值1.
故答案为:1.
点评 本题考查最值的求法,注意运用变形和导数,求得单调区间、极值和最值,考查化简整理的运算能力,属于难题.

| A. | $\frac{1}{3}$ | B. | $\frac{5}{12}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{2}$ |
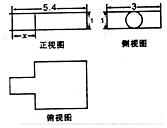 中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器-商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为13.5(立方寸),则图中的x为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器-商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为13.5(立方寸),则图中的x为( )| A. | 2.4 | B. | 1.8 | C. | 1.6 | D. | 1.2 |
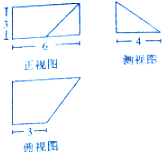
| A. | 36 | B. | 30 | C. | 24 | D. | 20 |
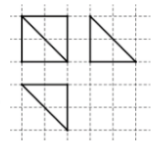 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体各面直角三角形的个数是( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体各面直角三角形的个数是( )