题目内容
17．已知某几何体的三视图如图所示，则该几何体的体积为（ ）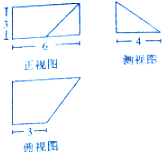
| A． | 36 | B． | 30 | C． | 24 | D． | 20 |
分析 由已知中的三视图，我们可以判断该几何体是由一个直三棱柱和一个四棱锥组成，分别求出棱柱和棱锥的体积，进而可得答案．
解答 解：由已知中的该几何体是由一个直三棱柱和一个四棱锥组成的组合体，
其中直三棱的底面为左视图，高为6-3=3，
故V直三棱柱=6×3=18，
四棱锥的底面为边长为3，4的长方体，高为4
故V四棱锥=$\frac{1}{3}$×3×4×3=12，
故该几何体的体积V=V直三棱柱+V四棱锥=30，
故选B．
点评 本题考查的知识点是由三视图求体积，其中根据三视图判断出几何体的形状，并找出棱长、高等关键的数据是解答本题的关键．
练习册系列答案
相关题目
5．已知正三角形ABC的三个顶点都在球心为O、半径为3的球面上，且三棱锥O-ABC的高为2，点D是线段BC的中点，过点D作球O的截面，则截面积的最小值为（ ）
| A． | $\frac{15π}{4}$ | B． | 4π | C． | $\frac{7π}{2}$ | D． | 3π |
12．已知一个几何体的三视图如图所示，则该几何体的表面积为（ ）
| A． | 4$\sqrt{2}$+6 | B． | 4$\sqrt{2}$+8 | C． | 4$\sqrt{2}$+12 | D． | 4$\sqrt{2}$+10 |
9．三棱锥S-ABC的所有顶点都在球O的表面上，SA⊥平面ABC，AB⊥AC，又SA=AB=AC=1，则球O的表面积为（ ）
| A． | $\frac{{\sqrt{3}}}{2}π$ | B． | $\frac{3}{2}π$ | C． | 3π | D． | 12π |
7．若实数x，y满足条件$\left\{\begin{array}{l}x≥1\\ x-2y+3≥0\\ y≥x\end{array}\right.$，则$z=\frac{y}{x+1}$的最小值为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | 1 |