Question

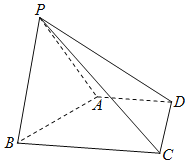
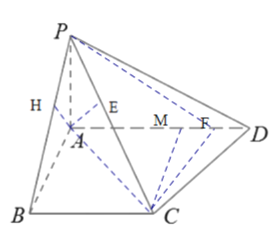
【题目】如图,在梯形ABCD中,AD//BC,∠ABC=，,∠ADC=，PA⊥平面ABCD且PA=.

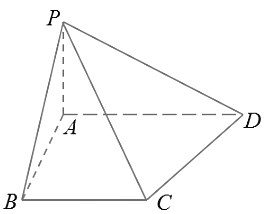
(1)求直线AD到平面PBC的距离；

(2)求出点A到直线PC的距离；

(3)在线段AD上是否存在一点F,使点A到平面PCF的距离为.

Answer 1

【答案】（1）（2）（3）存在，证明见解析.

【解析】

（1）直线AD到平面PBC的距离可转化为点A到平面PBC的距离，作于，可证明AH的长为点A到平面PBC的距离，求解即可（2）作于,则AE的长即为点A到PC的距离，利用三角形面积的等积法即可求解（3）假设存在点F，由（2）知只需平面，转化为是否存在即可求解.

（1） 作于，

由面ABCD，

，

，又，

平面PAB,

，又，

面PBC,

即AH的长为点A到平面PBC的距离，也即直线AD到平面PBC的距离，

在等腰中，，

所以直线AD到平面PBC的距离为.

（2）作于,则AE的长即为点A到PC的距离.

在中， ，

,

即点A到直线PC的距离为.

（3）假设在线段AD上是存在一点F，使点A到平面PCF的距离为，

设

过C作于M，在中，,

可得,，

所以，

由（2）知，若存在F,使得平面即可,

由条件可知，只需,则平面

设，则，

在中，由余弦定理可得，

若，在中，

,

即，

解得，

即在AD上存在一点F，当时，

，

又,,

平面，

，又，,

平面,即点A到平面PCF的距离为，

此时满足条件.