题目内容
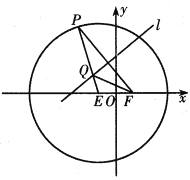
【题目】如图,已知圆![]() ,点
,点![]() 是圆
是圆![]() 内一个定点,
内一个定点,![]() 是圆
是圆![]() 上任意-一点,线段
上任意-一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() ,连接
,连接![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 、
、![]() 是曲线
是曲线![]() 上关于原点对称的两个点,点
上关于原点对称的两个点,点![]() 是曲线
是曲线![]() .上任意-一点(不同于点
.上任意-一点(不同于点![]() 、
、![]() ),当直线
),当直线![]() 、
、![]() 的斜率都存在时,记它们的斜率分别为
的斜率都存在时,记它们的斜率分别为![]() 、
、![]() ,求证:
,求证:![]() 的为定值.
的为定值.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)根据中垂线的性质可得![]() ,可得
,可得![]() ,由椭圆的定义知,
,由椭圆的定义知,![]() 点的轨迹是以
点的轨迹是以![]() ,
,![]() 为焦点,长轴长为4的椭圆,即可求出轨迹方程.
为焦点,长轴长为4的椭圆,即可求出轨迹方程.
(2)设![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,表示出
,表示出
![]() 、
、![]() ,由
,由![]() 、
、![]() 、
、![]() 在椭圆上,则满足椭圆方程,消去
在椭圆上,则满足椭圆方程,消去![]() 即可得
即可得![]() 为一个定值.
为一个定值.
(1)解:![]() 在线段
在线段![]() 的中垂线
的中垂线![]() 上,
上,
![]() ,
,
![]() ,
,
又![]()
![]() 点的轨迹是以
点的轨迹是以![]() ,
,![]() 为焦点,长轴长为4的椭圆,
为焦点,长轴长为4的椭圆,
![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
![]() ,
,
![]() 曲线
曲线![]() 的方程为
的方程为![]() .
.
(2)设曲线![]() 上点
上点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
故![]() ,
,![]() ,
,
由斜率公式得![]() ,
,![]()
![]()
又![]() ,
,![]() ,
,
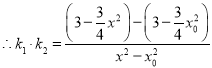
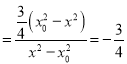
因此,斜率之积![]() 为定值
为定值![]() .
.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
【题目】一次考试中,5名同学的数学、物理成绩如表所示:
学生 |
|
|
|
|
|
数学 | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
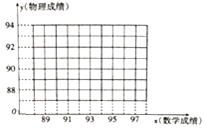
![]() 请在图中的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
请在图中的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
![]() 要从4名数学成绩在90分以上的同学中选2名参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望
要从4名数学成绩在90分以上的同学中选2名参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望![]() .
.
参考公式:线性回归方程![]() ;,其中
;,其中![]() ,
,![]() .
.