题目内容
6.已知曲线C1的参数方程为$\left\{\begin{array}{l}x=4+5cost\\ y=5+5sint\end{array}\right.$(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
分析 (1)曲线C1的参数方程消去参数t,得到普通方程,再由$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$,能求出C1的极坐标方程.
(2)曲线C2的极坐标方程化为直角坐标方程,与C1的普通方程联立,求出C1与C2交点的直角坐标,由此能求出C1与C2交点的极坐标.
解答 解:(1)将$\left\{\begin{array}{l}{x=4+5cost}\\{y=5+5sint}\end{array}\right.$,消去参数t,化为普通方程(x-4)2+(y-5)2=25,
即C1:x2+y2-8x-10y+16=0,
将$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入x2+y2-8x-10y+16=0,
得ρ2-8ρcosθ-10ρsinθ+16=0.
∴C1的极坐标方程为ρ2-8ρcosθ-10ρsinθ+16=0.
(2)∵曲线C2的极坐标方程为ρ=2sinθ.
∴曲线C2的直角坐标方程为x2+y2-2y=0,
联立$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}-8x-10y+16=0}\\{{x}^{2}+{y}^{2}-2y=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$,
∴C1与C2交点的极坐标为($\sqrt{2},\frac{π}{4}$)和(2,$\frac{π}{2}$).
点评 本题考查曲线极坐标方程的求法,考查两曲线交点的极坐标的求法,考查极坐标方程、直角坐标方程、参数方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案| A. | (1,0),(0,-2) | B. | (0,1),(-1,0) | C. | (0,-1),(1,0) | D. | (0,3),(-3,0) |

| A. | 2π | B. | $\frac{3π}{2}$ | C. | $\frac{4π}{3}$ | D. | $\frac{7π}{6}$ |
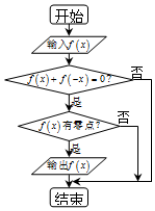 某流程图如图所示,现输入如下四个函数,则可以输出的函数是①②③.
某流程图如图所示,现输入如下四个函数,则可以输出的函数是①②③.