题目内容
4.己知不等式|x一1|≤1的解集为A,关于x的不等式$\frac{x-a}{x+1}$<0的解集为B,(1)当a=1时,求集合A∪B;
(2)若对于任意的实数x0∈A,都有x0∈B,求实数a的取值范围.
分析 (1)由绝对值不等式的解法求出集合A,把a=1代入不等式,由分式不等式、一元二次不等式的解法求出集合B,由并集的运算求出A∪B;
(2)由条件可得A⊆B,将分式不等式转化后,对a分类讨论,分别由子集的定义,求出实数a的取值范围.
解答 解:(1)由|x-1|≤1得-1≤x-1≤1,解得0≤x≤2,
则集合A=[0,2],
当a=1时,不等式$\frac{x-a}{x+1}<0$化为(x+1)(x-1)<0,
解得-1<x<1,则B=(-1,1),
∴A∪B=(-1,2];
(2)∵对于任意的实数x0∈A,都有x0∈B,
∴A⊆B,即[0,2]⊆B,
不等式$\frac{x-a}{x+1}<0$化为(x+1)(x-a)<0,
①当a≤-1时,不满足A⊆B;
②当a>-1时,集合B=(-1,a),
∵[0,2]⊆(-1,a),∴a>2,
∴实数a的取值范围是(2,+∞).
点评 本题考查绝对值不等式、分式不等式的等价转化及解法,一元二次不等式的解法,考查分类讨论思想,转化思想,化简、变形能力.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
8.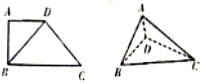 如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使得平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体中,下列说法正确的是( )
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使得平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体中,下列说法正确的是( )
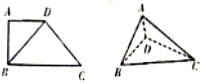 如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使得平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体中,下列说法正确的是( )
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使得平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体中,下列说法正确的是( )| A. | 平面ABD⊥平面ABC | B. | 平面ACD⊥平面BCD | C. | 平面ABC⊥平面BCD | D. | 平面ACD⊥平面ABC |
6.命题p:方程$\frac{x^2}{5-m}+\frac{y^2}{m-1}=1$表示焦点在y轴上的椭圆,则使命题p成立的充分不必要条件是( )
| A. | 4<m<5 | B. | 3<m<5 | C. | 1<m<5 | D. | 1<m<3 |
9.祖暅原理:“幂势既同,则积不容异”.它是中国古代一个涉及几何体体积的问题,意思是两个同高的几何体,如在等高处的截面积恒相等,则体积相等.设A、B为两个同高的几何体,p:A、B的体积不相等,q:A、B在等高处的截面积不恒相等,根据祖暅原理可知,p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.函数f(x)=2x-8+log3x的零点一定位于区间( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (5,6) |
 抛物线y2=4x的焦点为F,斜率为1的直线l过点F,且与抛物线相交于A,B两点,M是AB中点.
抛物线y2=4x的焦点为F,斜率为1的直线l过点F,且与抛物线相交于A,B两点,M是AB中点.