题目内容
设集合M={-1，0，1}，N={x|x2≤x}，M∩N=（ ）
| A、{0} |
| B、{0，1} |
| C、{-1，1} |
| D、{-1，0} |
考点：交集及其运算
专题：集合
分析：求出N中不等式的解集确定出N，找出M与N的交集即可．
解答：
解：由N中不等式变形得：x（x-1）≤0，
解得：0≤x≤1，即N=[0，1]，
∵M={-1，0，1}，
∴M∩N={0，1}，
故选：B．
解得：0≤x≤1，即N=[0，1]，
∵M={-1，0，1}，
∴M∩N={0，1}，
故选：B．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
在△ABC中，A：B：C=1：2：3，则a：b：c等于（ ）
| A、1：2：3 | ||
| B、3：2：1 | ||
C、1：
| ||
D、2：
|
下列函数与y=
是同一函数的是（ ）
| 1 |
| x |
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=aloga
|
函数f（x）=
的定义域为（ ）
| x-2 |
| A、（2，+∞） |
| B、（+∞，2） |
| C、（-∞，2] |
| D、[2，+∞） |
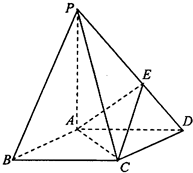如图，在底面为棱形的四棱锥P-ABCD在那个，∠ABC=60°，PA=AC=1，PB=PD=| 2 |
（1）求证：PA⊥平面ABCD；
（2）求二面角E-AC-D的正弦值．
椭圆
+
=1（a＞b＞0）上一点A关于原点的对称点为B，!F为其左焦点，若AF⊥BF，设∠ABF=
，则该椭圆的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、1-
|
在空间中，a，b是不重合的直线，α，β是不重合的平面，则下列条件中可推出a∥b的是（ ）
| A、a?α，b?β，α∥β |
| B、a∥α，b?β |
| C、a⊥α，b⊥β |
| D、a⊥α，b?α |