题目内容

18．某几何体的三视图如图所示，则它的表面积为（　　）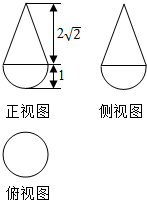
A．6πB．5πC．4πD．3π

分析 根据几何体的三视图，得出该几何体是圆锥与半球体的组合体，结合图中数据求出它的表面积．

解答 解：根据几何体的三视图，得；
该几何体是圆锥与半球体的组合体，
且圆锥的高为2$\sqrt{2}$，底面圆的半径为1，球的半径也为1，
圆锥的母线长为$\sqrt{{（2\sqrt{2}）}^{2}{+1}^{2}}$=3；
所以，该几何体的表面积为
S=S圆锥侧+S半球
=π×1×3+2π×12
=5π．
故选：B．

点评 本题考查了利用几何体三视图求表面积的应用问题，是基础题目．

练习册系列答案
相关题目
8．已知函数f（x）=xm过点（2，$\frac{1}{2}$），则m=-1．
9．复数$\frac{2-i}{1-i}$的共轭复数是（　　）
A．$\frac{3+i}{2}$B．$\frac{1-i}{2}$C．$\frac{3-i}{2}$D．$\frac{-3-i}{2}$
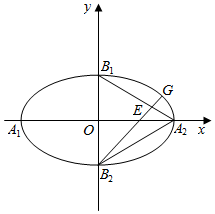6．（1）计算${（5\frac{1}{16}）^{0.5}}-2×{（2\frac{10}{27}）^{-\frac{2}{3}}}-2×{（\sqrt{2+π}）^0}÷{（\frac{3}{4}）^{-2}}$
（2）计算${9^{{{log}_3}2}}-4{log_4}3•{log_{27}}8+\frac{1}{3}{log_6}8-2{log_{{6^{-1}}}}\sqrt{3}$．
13．如图，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的四个顶点是A1，A2，B1，B2，△A2B1B2是边长为2的正三角形．
（1）求椭圆的方程；
（2）若G是椭圆上在第一象限内的动点，直线B1G交线段A2B2于点E，求$\frac{|G{B}_{1}|}{|E{B}_{1}|}$的取值范围．
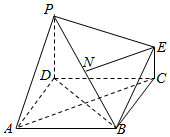3．如图为一简单组合体，其底面ABCD为正方形，棱PD与EC均垂直于底面ABCD，PD=2EC，N为PB的中点，求证：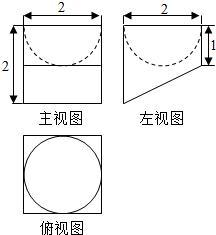
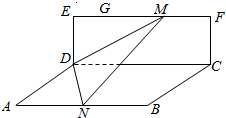（1）平面EBC∥平面PDA；
（2）NE⊥平面PDB．
10．某几何体的三视图如图所示，则该几何体的体积是6-$\frac{2π}{3}$．
7．设F1、F2分别是椭圆E：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{b}$=1（b＞0）的左、右焦点．若P是椭圆E上的一个动点．且$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$的最大值为1．
（1）求椭圆E的方程；
（2）设直线x=ky-1与椭圆E交于A、B两点，点A关于x轴的对称点为A′（A′与B不重合）．则直线A′B与x轴是否交于一个定点？若是，请写出该定点的坐标，并证明你的结论；若不是．请说明理由．
8．如图，矩形CDEF所在的平面与矩ABCD所在的平面垂直，AD=$\sqrt{2}$，DE=$\sqrt{3}$，AB=4，$\overrightarrow{EG}$=$\frac{1}{4}$$\overrightarrow{EF}$，点M在线段GF上（包括两端点），点N在线段AB上，且$\overrightarrow{GM}$=$\overrightarrow{AN}$，则二面角M-DN-B的平面角的取值范围为[$\frac{π}{4}$，$\frac{π}{3}$]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网