题目内容
8.直线3x-4y+2=0的单位法向量$\overrightarrow{n_0}$=$±(\frac{3}{5},\frac{4}{5})$.分析 设单位法向量$\overrightarrow{n_0}$=(a,b),可得3b-4a=0,又$\sqrt{{a}^{2}+{b}^{2}}$=1,联立解出即可得出.
解答 解:设单位法向量$\overrightarrow{n_0}$=(a,b),则3b-4a=0,
又$\sqrt{{a}^{2}+{b}^{2}}$=1,
联立解得$\left\{\begin{array}{l}{a=\frac{3}{5}}\\{b=\frac{4}{5}}\end{array}\right.$,或$\left\{\begin{array}{l}{a=-\frac{3}{5}}\\{b=-\frac{4}{5}}\end{array}\right.$,
∴单位法向量$\overrightarrow{n_0}$=$±(\frac{3}{5},\frac{4}{5})$.
故答案为:$±(\frac{3}{5},\frac{4}{5})$.
点评 本题考查了向量垂直于数量积的关系、单位向量,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.已知全集U=R,A={x|x2-5x+6≥0},则∁UA=( )
| A. | {x|x>2} | B. | {x|x>3或x<2} | C. | {x|2≤x≤3} | D. | {x|2<x<3} |
13.已知坐标原点O(0,0)关于直线L对称的点是M(3,-3),则直线L的方程是( )
| A. | x-2y+1=0 | B. | 2x-y-1=0 | C. | x-y+3=0 | D. | x-y-3=0 |
18.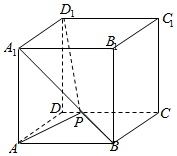 如图棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )
如图棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )
 如图棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )
如图棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )| A. | 平面D1A1P⊥平面A1AP | B. | 二面角B-A1D1-A的大小为45° | ||
| C. | 三棱锥B1-D1PC的体积不变 | D. | AP+PD1的最小值为$\sqrt{2+\sqrt{3}}$ |
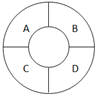 如图,一环形花坛分成A、B、C、D四块,现有4种不同的花供选种,要求在每块里种一种花,且相邻的2块种不同的花,则不同的种法总数为84.
如图,一环形花坛分成A、B、C、D四块,现有4种不同的花供选种,要求在每块里种一种花,且相邻的2块种不同的花,则不同的种法总数为84.