题目内容
2.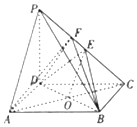 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为矩形,E为PC的中点,且$PD=AD=\frac{1}{2}AB=4$.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为矩形,E为PC的中点,且$PD=AD=\frac{1}{2}AB=4$.(1)过点A作一条射线AG,使得AG∥BD,求证:平面PAG∥平面BDE;
(2)若点F为线段PC上一点,且DF⊥平面PBC,求四棱锥F-ABCD的体积.
分析 (1)在矩形ABCD中,连结AC和BD交于点O,连接OE,则O是AC的中点,从而OE∥PA,进而PA∥平面BDE,由AG∥BD,得AG∥平面BDE,由此能证明平面PAG∥平面BDE.
(2)由DF⊥PC,过F作FK∥PD,交CD于K,则FK⊥底面ABCD,由此能求出四棱锥F-ABCD的体积.
解答 证明:(1)在矩形ABCD中,连结AC和BD交于点O,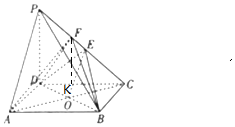
连接OE,则O是AC的中点,
∵E是PC的中点,∴OE是△PAC的中位线,∴OE∥PA,
又OE?平面BDE,PA?平面BDE,
∴PA∥平面BDE,
又AG∥BD,同理得AG∥平面BDE,
∵PA∩AG=A,∴平面PAG∥平面BDE.
解:(2)∵DF⊥平面PBC,∴DF⊥PC.
在Rt△PDC中,∵PD=4,CD=8,∴$PC=4\sqrt{5}$,
∴DF=$\frac{4×8}{4\sqrt{5}}$=$\frac{8\sqrt{5}}{5}$,∴FC=$\sqrt{C{D}^{2}-D{F}^{2}}$=$\frac{16\sqrt{5}}{5}$,∴$\frac{FC}{PC}$=$\frac{4}{5}$,
过F作FK∥PD,交CD于K,则FK=$\frac{4}{5}×4=\frac{16}{5}$,
∵PD⊥底面ABCD,∴FK⊥底面ABCD,
∴${V_{F-ABCD}}=\frac{1}{3}×\frac{16}{5}×4×8=\frac{512}{15}$.
点评 本题考查面面平行的证明,考查四棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
10.不等式组$\left\{\begin{array}{l}{2x-y+1≥0}\\{x-2y+2≤0}\\{x+y-4≤0}\end{array}\right.$的解集记作D,实数x,y满足如下两个条件:①?(x,y)∈D,y≥ax;②?(x,y)∈D,x-y≤a.则实数a的取值范围为( )
| A. | [-2,1] | B. | [0,1] | C. | [-2,3] | D. | [0,3] |
8.已知O为坐标原点,F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,双曲线C上一点P满足PF1⊥PF2,且|PF1||PF2|=2a2,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
7.下列函数中,在区间(0,+∞)上单调递增且为偶函数的是( )
| A. | y=x3 | B. | y=2x | ||
| C. | y=[x](不超过x的最大整数) | D. | y=|x| |