题目内容
 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC的中点.(Ⅰ)求证:EF∥平面PAB;
(Ⅱ)求直线EF与平面ABE所成角的大小.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角,空间向量及应用
分析:(Ⅰ)取PA中点M,AB中点N,连接MN,NF,ME,容易证明四边形MNFE为平行四边形,所以EF∥MN,所以得到EF∥平面PAB;
(Ⅱ)分别以向量
,
,
的方向为x轴,y轴,z轴的正方向建立空间直角坐标系A-xyz.可以确定点P,A,B,C,D,E,F的坐标,从而确定向量
,
,
的坐标,设平面ABE的法向量为
=(a,b,c),根据
⊥
,
⊥
即可求得一个法向量,根据法向量和向量
的夹角和EF与平面ABE所成的角的关系即可求出所求的角.
(Ⅱ)分别以向量
| AB |
| AD |
| AP |
| EF |
| AE |
| AB |
| n |
| n |
| AE |
| n |
| AB |
| EF |
解答:
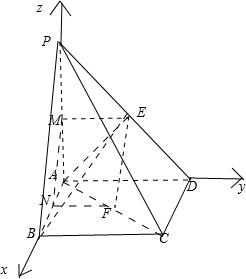 解:(Ⅰ)证明:分别取PA和AB中点M,N,连接MN、ME、NF,则NF∥AD,且NF=
解:(Ⅰ)证明:分别取PA和AB中点M,N,连接MN、ME、NF,则NF∥AD,且NF=
AD,ME∥AD,且ME=
AD,所以NF∥ME,且NF=ME所以四边形MNFE为平行四边形;
∴EF∥MN,又EF?平面PAB,MN?平面PAB,∴EF∥平面PAB;
(Ⅱ)由已知:底面ABCD为正方形,侧棱PA⊥底面ABCD,所以AP,AB,AD两两垂直;
如图所示,以A为坐标原点,分别以
,
,
为x轴,y轴,z轴的正方向,建立空间直角坐标系A-xyz,所以:
P(0,0,1),A(0,0,0,),B(1,0,0),C(1,1,0),D(0,1,0),E(0,
,
),F(
,
,0);
∴
=(
,0,-
),
=(0,
,
),
=(1,0,0);
设平面ABE法向量
=(a,b,c),则
•
=0,
•
=0;
∴
令b=1,则c=-1,a=0;
∴
=(0,1,-1)为平面ABE的一个法向量;
设直线EF与平面ABE所成角为α,于是:
sinα=|cos<
,
>|=|
|=
;
所以直线EF与平面ABE所成角为
.
 解:(Ⅰ)证明:分别取PA和AB中点M,N,连接MN、ME、NF,则NF∥AD,且NF=
解:(Ⅰ)证明:分别取PA和AB中点M,N,连接MN、ME、NF,则NF∥AD,且NF=| 1 |
| 2 |
| 1 |
| 2 |
∴EF∥MN,又EF?平面PAB,MN?平面PAB,∴EF∥平面PAB;
(Ⅱ)由已知:底面ABCD为正方形,侧棱PA⊥底面ABCD,所以AP,AB,AD两两垂直;
如图所示,以A为坐标原点,分别以
| AB |
| AD |
| AP |
P(0,0,1),A(0,0,0,),B(1,0,0),C(1,1,0),D(0,1,0),E(0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| AE |
| 1 |
| 2 |
| 1 |
| 2 |
| AB |
设平面ABE法向量
| n |
| n |
| AE |
| n |
| AB |
∴
|
∴
| n |
设直线EF与平面ABE所成角为α,于是:
sinα=|cos<
| EF |
| n |
| ||||
|
|
| 1 |
| 2 |
所以直线EF与平面ABE所成角为
| π |
| 6 |
点评:考查线面平行的判定定理,通过建立空间直角坐标系,用向量的方法求一直线和平面所成的角,以及两非零向量垂直的充要条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
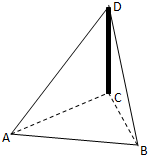 如图所示,哈三中甲,乙两位同学分别站在新校区体育场内的A,B两点,利用三角函数知识测量锅炉房烟囱CD的高.已知AB=15米,∠DAC=60°,∠CAB=15°,∠CBA=45°,求烟囱CD的高.
如图所示,哈三中甲,乙两位同学分别站在新校区体育场内的A,B两点,利用三角函数知识测量锅炉房烟囱CD的高.已知AB=15米,∠DAC=60°,∠CAB=15°,∠CBA=45°,求烟囱CD的高. 已知四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,且PD=AB=2.
已知四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,且PD=AB=2.