题目内容
若函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈[-1,1]时,f(x)=1-|x|,函数g(x)=
,则函数h(x)=f(x)-g(x)在区间[-4,4]内的零点个数是 .
|
考点:函数零点的判定定理,分段函数的应用
专题:函数的性质及应用
分析:由f(x+2)=f(x),得y=f(x)是周期为2的周期函数,画出函数f(x),g(x)的图象,通过图象求出两个函数的交点,从而求出函数f(x)的零点.
解答:
解:∵f(x+2)=f(x),
∴y=f(x)是周期为2的周期函数,
∵x∈[-1,1]时,f(x)=1-|x|,
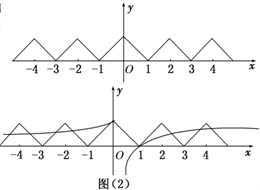
函数f(x)的图象如图中所示,
而函数h(x)=f(x)-g(x)在区间[-4,4]内
的零点个数是函数f(x)与g(x)的交点个数,
如图示:
 ,
,
由图象可知:在[-4,0]上有4个交点,
在(0,4]上有3个交点,
∴f(x)与g(x)共有7个交点,
∴函数h(x)共有7个零点.,
故答案为:7个.
∴y=f(x)是周期为2的周期函数,
∵x∈[-1,1]时,f(x)=1-|x|,
函数f(x)的图象如图中所示,
而函数h(x)=f(x)-g(x)在区间[-4,4]内
的零点个数是函数f(x)与g(x)的交点个数,
如图示:
 ,
,由图象可知:在[-4,0]上有4个交点,
在(0,4]上有3个交点,
∴f(x)与g(x)共有7个交点,
∴函数h(x)共有7个零点.,
故答案为:7个.
点评:本题考察了函数的零点问题,渗透了转化思想,数形结合思想,是一道基础题.

练习册系列答案
相关题目
某程序的框图如图所示,执行该程序,若输入的E为0.96,则输出的K为( )


| A、20 | B、22 | C、24 | D、25 |
