题目内容
9.执行如图所示的程序框图,则输出的S的值为( )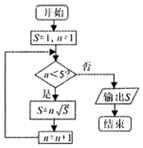
| A. | $4\sqrt{3\sqrt{2}}$ | B. | $5\sqrt{4\sqrt{3\sqrt{2}}}$ | C. | $5\sqrt{4}$ | D. | $4\sqrt{3}$ |
分析 模拟程序的运行,依次写出每次循环得到的S,n的值,当n=5时不满足条件n<5,退出循环,输出S的值4$\sqrt{3\sqrt{2}}$.
解答 解:模拟程序的运行,可得
S=1,n=1
满足条件n<5,执行循环体,S=1,n=2
满足条件n<5,执行循环体,S=2,n=3
满足条件n<5,执行循环体,S=3$\sqrt{2}$,n=4
满足条件n<5,执行循环体,S=4$\sqrt{3\sqrt{2}}$,n=5
不满足条件n<5,退出循环,输出S的值4$\sqrt{3\sqrt{2}}$.
故选:A.
点评 本题主要考查了循环结构的程序框图的应用,当循环次数有限或有规律时常采用模拟程序运行的方法来解决,属于基础题.

练习册系列答案
相关题目
20.已知三棱锥P-ABC的三条侧棱两两互相垂直,且AB=$\sqrt{5}$,BC=$\sqrt{7}$,AC=2,则此三棱锥的外接球的体积为( )
| A. | $\frac{8}{3}$π | B. | $\frac{8\sqrt{2}}{3}$π | C. | $\frac{16}{3}$π | D. | $\frac{32}{3}$π |
17.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x+2y+2≥0}\\{2x-y+2≤0}\\{x≤0}\end{array}\right.$,则z=3x-y的最大值为( )
| A. | 1 | B. | -$\frac{16}{5}$ | C. | -2 | D. | 不存在 |
4.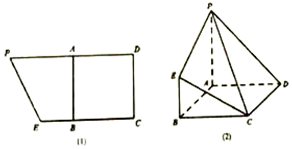 已知梯形CEPD如图(1)所示,其中PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,得到如图(2)所示的几何体.已知当点F满足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$(0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( )
已知梯形CEPD如图(1)所示,其中PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,得到如图(2)所示的几何体.已知当点F满足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$(0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( )
 已知梯形CEPD如图(1)所示,其中PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,得到如图(2)所示的几何体.已知当点F满足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$(0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( )
已知梯形CEPD如图(1)所示,其中PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,得到如图(2)所示的几何体.已知当点F满足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$(0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
3.函数f(x)=x3+x-2有 ( )个零点.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
20.已知函数f(x)=3ax4-2(3a+1)x2+4x,在(-1,1)上是增函数,求a的取值范围( )$.
| A. | [-$\frac{4}{3}$,$\frac{1}{6}$] | B. | (0,$\frac{1}{6}$] | C. | (0,$\frac{1}{6}$) | D. | (-$\frac{4}{3}$,$\frac{1}{6}$) |
1. 若二次函数f(x)的图象与x轴有两个异号交点,它的导函数f'(x)的图象如图所示,则函数f(x)图象的顶点在( )
若二次函数f(x)的图象与x轴有两个异号交点,它的导函数f'(x)的图象如图所示,则函数f(x)图象的顶点在( )
 若二次函数f(x)的图象与x轴有两个异号交点,它的导函数f'(x)的图象如图所示,则函数f(x)图象的顶点在( )
若二次函数f(x)的图象与x轴有两个异号交点,它的导函数f'(x)的图象如图所示,则函数f(x)图象的顶点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |