题目内容
17.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x+2y+2≥0}\\{2x-y+2≤0}\\{x≤0}\end{array}\right.$,则z=3x-y的最大值为( )| A. | 1 | B. | -$\frac{16}{5}$ | C. | -2 | D. | 不存在 |
分析 首先画出平面区域,利用目标函数的几何意义求最大值.
解答 解:不等式组表示的平面区域如图: 目标函数z=3x-y变形为y=3x-z,
目标函数z=3x-y变形为y=3x-z,
此直线在y轴截距最小时,z最大,
由区域可知,直线经过图中A(0,2)时,z取最大值为-2;
故选C
点评 本题考查了简单线性规划问题;首先正确画出可行域,利用目标函数的几何意义求最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若集合A={-1,0,1},B={y|y=x2,x∈A},则A∩B=( )
| A. | {0} | B. | {1} | C. | {0,1} | D. | {0,-1} |
9.执行如图所示的程序框图,则输出的S的值为( )
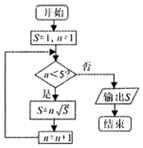

| A. | $4\sqrt{3\sqrt{2}}$ | B. | $5\sqrt{4\sqrt{3\sqrt{2}}}$ | C. | $5\sqrt{4}$ | D. | $4\sqrt{3}$ |
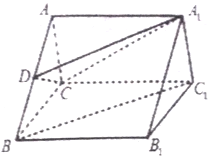 如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,过A1C作平面A1CD平行于BC1,交AB于D点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,过A1C作平面A1CD平行于BC1,交AB于D点.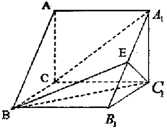 如图,三棱柱ABC-A1B1C1中,A1C1⊥BB1,AC=BC=BB1,E为A1B1的中点,且C1E⊥BB1.
如图,三棱柱ABC-A1B1C1中,A1C1⊥BB1,AC=BC=BB1,E为A1B1的中点,且C1E⊥BB1.