题目内容
17．设全集U=R，若集合A={x||x-1|＞1}，则∁UA=[0，2]．分析 求出集合A，利用集合的基本运算即可得到结论．
解答 解：|x-1|＞1，
∴x-1＞1或x-1＜-1，
∴x＞2或x＜0，
∴A=（-∞，0）∪（2，+∞），
∴∁UA=[0，2]，
故答案为：=[0，2]．
点评 本题主要考查集合的基本运算，比较基础．
练习册系列答案
相关题目
8．以（-3，0）和（3，0）为焦点，长轴长为8的椭圆方程为（ ）
| A． | $\frac{x^2}{16}+\frac{y^2}{25}=1$ | B． | $\frac{x^2}{16}+\frac{y^2}{7}=1$ | C． | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | D． | $\frac{x^2}{7}+\frac{y^2}{16}=1$ |
5．若全集U=R，集合A={x|x2+4x+3＞0}，B={x|log3（2-x）≤1}，则∁U（A∩B）=（ ）
| A． | {x|x＜-1或x＞2} | B． | {x|x＜-1或x≥2} | C． | {x|x≤-1或x＞2} | D． | {x|x≤-1或x≥2} |
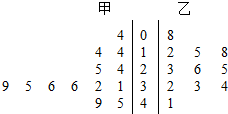现今社会对食品安全的高度重视，各级政府加强了对食品安全的检查力度．某市工商质检局抽派甲、乙两个食品质量检查组到管辖区域内的商店进行食品质量检查．如图表示甲、乙两个检查组每天检查到的食品品种数的茎叶图，则甲、乙两个检查组每天检查到的食品种数的中位数的和是58．