题目内容

函数y=3cos2x-4sinx+1的最大值为
 
，最小值为
 
．
考点：三角函数的最值
专题：三角函数的求值
分析：先把函数转化成关于sinx的函数，利用换元法和二次函数的性质确定函数的最大和最小值．
解答： 解：y=3cos2x-4sinx+1=-3sin2x-4sinx+4，设t=sinx．-1≤t≤1，
y=-3t2-4t+4，对称轴为t=
2
3
，
∴ymax=f（
2
3
）=
16
3
，
ymin=f（1）=-3．
故答案为：
16
3
，-3．
点评：本题主要考查了二次函数的性质，三角函数求最值的问题．解题的过程中注意与二次函数的图象相结合．
练习册系列答案
相关题目
重庆市某知名中学高三年级甲班班主任近期对班上每位同学的成绩作相关分析时，得到石周卓婷同学的某些成绩数据如下：
第一次考试 第二次考试 第三次考试 第四次考试
数学总分 118 119 121 122
总分年级排名 133 127 121 119
（1）求总分年级名次对数学总分的线性回归方程y=bx+a；（必要时用分数表示）
（2）若石周卓婷同学想在下次的测试时考入前100名，预测该同学下次测试的数学成绩至少应考多少分（取整数，可四舍五入）．附：线性回归方程y=bx+a中，b=
n
i=1
(xi-
.
x
)(yi-
.
y
)
n
i=1
(xi-
.
x
)2
，a=
.
y
-b
.
x
．
已知圆C的圆心在坐标原点，且过点M（1 ， 
3
）．
（1）求圆C的方程；
（2）已知点P是圆C上的动点，试求点P到直线x+y-4=0的距离的最小值；
（3）若直线l与圆C相切于点M，求直线l的方程．
某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40，50）、[50，60）、[60，70）、[70，80）、[90，100）、[90，100]．
（Ⅰ）求图中x的值及平均成绩；
（Ⅱ）从成绩不低于80分的学生中随机选取2人，求2人成绩都不低于90分的概率．
求值cos
π
7
cos
2π
7
cos
4π
7
=
 
．
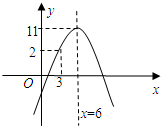某汽车运输公司，购买了一批豪华大客车投入客运，据市场分析，每辆客车营运的总利润y（万元）与营运年数x（x∈N*）的二次函数关系如图，为了使每辆客车营运的年平均利润最大，则每辆客车应营运
 
年．
若实数x，y满足 x2+y2-2x-2y+1=0，则
x-2
y-4
的取值范围为
 
．
不等式x2＜1的解集为
 
．
如图所示，一组数排成倒三角形，其中第一行各数依次为1，2，3，…10，从第二行起，每一个数都等于他“肩上”的两个数之和，最后一行只有一个数M，则M=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网