题目内容
已知函数f（x）=
的定义域是一切实数，则m的取值范围是（ ）
| mx2+mx+1 |
| A、0＜m≤4 | B、0≤m≤1 |
| C、m≥4 | D、0≤m≤4 |
考点：函数恒成立问题,函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数的定义域是全体实数，得到mx2+mx+1≥0恒成立，即可得到结论．
解答：
解：若函数f（x）=
的定义域是一切实数，
则等价为mx2+mx+1≥0恒成立，
若m=0，则不等式等价为1≥0，满足条件，
若m≠0，则满足
，
即
，
解得0＜m≤4，
综上0≤m≤4，
故选：D
| mx2+mx+1 |
则等价为mx2+mx+1≥0恒成立，
若m=0，则不等式等价为1≥0，满足条件，
若m≠0，则满足
|
即
|
解得0＜m≤4，
综上0≤m≤4，
故选：D
点评：本题主要考查函数恒成立，结合一元二次不等式的性质是解决本题的关键．
练习册系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
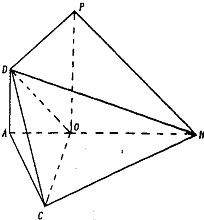如图，在△ABC中，已知∠ABC=45°，O在AB上，且OB=OC=| 2 |
| 3 |
| 1 |
| 2 |
（I）求证：PB∥平面COD；
（II）求二面角O-CD-A的余弦值．
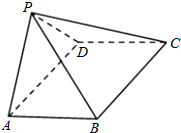如图，四棱锥P-ABCD中，ABCD为矩形，平面PAD⊥平面ABCD．