题目内容
3.曲线y=x3-2x+m在x=1处的切线斜率等于1.分析 根据导数的几何意义可知k=y′|x=1,即可得出结论.
解答 解:y′=3x2-2,切线的斜率k=3×12-2=1,
故答案为1.
点评 本题考查了导数的几何意义,考查学生的计算能力,本题属于容易题.

练习册系列答案
相关题目
13.函数y=$\frac{\sqrt{x+1}}{x}$的定义域是( )
| A. | [-1,+∞) | B. | [-1,0) | C. | (-1,+∞) | D. | {x|x≥-1,且x≠0} |
11.已知命题p:若x<-3,则x2-2x-8>0,则下列叙述正确的是( )
| A. | 命题p的逆命题是:若x2-2x-8≤0,则x<-3 | |
| B. | 命题p的否命题是:若x≥-3,则x2-2x-8>0 | |
| C. | 命题p的否命题是:若x<-3,则x2-2x-8≤0 | |
| D. | 命题p的逆否命题是真命题 |
18.设$a=(\frac{7}{9})^{5}$,$b=(\frac{9}{7})^{\frac{1}{5}}$,$c=lo{g}_{2}\frac{7}{9}$,则a,b,c的大小关系是( )
| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
12.定义在R上的函数f(x),已知函数y=f(x+1)的图象关于直线x=-1对称,对任意的x1,x2∈(-∞,0)(x1≠x2),都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}<0$,则下列结论正确的是( )
| A. | f(0.32)<f(20.3)<f(log25) | B. | $f({log_2}5)<f({2^{0.3}})<f({0.3^2})$ | ||
| C. | $f({log_2}5)<f({0.3^2})<f({2^{0.3}})$ | D. | $f({0.3^2})<f({log_2}5)<f({2^{0.3}})$ |
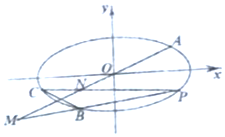 如图,在平面直角坐标系xOy中,已知A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上不同的三点,$A(\sqrt{10},\frac{{\sqrt{10}}}{2})$,B(-2,-2),C在第三象限,线段BC的中点在直线OA上.
如图,在平面直角坐标系xOy中,已知A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上不同的三点,$A(\sqrt{10},\frac{{\sqrt{10}}}{2})$,B(-2,-2),C在第三象限,线段BC的中点在直线OA上.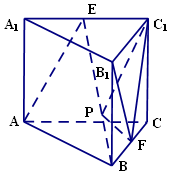 在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.
在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.