题目内容
已知曲线C的极坐标方程为:ρ2=2ρcosθ-mρsinθ+4上的两点M、N关于直线
(t为参数)对称,则m= ;直线l:tx+y-t+1=0(t∈R)与曲线C相交于A、B两点,则|AB|的最小值是 .(注:极坐标系的极轴OX与直角坐标系的X轴的非负半轴重合且单位长度相同)
|
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:化圆的极坐标方程为直角坐标方程,求出圆心和半径,化直线的参数方程为普通方程,把圆心坐标代入直线方程求得m的值;求出圆的方程,利用直线l:tx+y-t+1=0过定点得到圆心到直线的距离的最大值,由勾股定理求得|AB|的最小值.
解答:
解:由ρ2=2ρcosθ-mρsinθ+4,得
x2+y2=2x-my+4,即(x-1)2+(y+
)2=5+
.
由
,得2x+y=0.
∵圆关于直线对称,
∴2×1-
=0,解得m=4.
∴圆的方程为:(x-1)2+(y+2)2=9.
直线l:tx+y-t+1=0恒过定点(1,-1),
圆心(1,-2)到直线l:tx+y-t+1=0的最大值为1.
∴|AB|的最小值是2
=4
.
故答案为:4,4
.
x2+y2=2x-my+4,即(x-1)2+(y+
| m |
| 2 |
| m2 |
| 4 |
由
|
∵圆关于直线对称,
∴2×1-
| m |
| 2 |
∴圆的方程为:(x-1)2+(y+2)2=9.
直线l:tx+y-t+1=0恒过定点(1,-1),
圆心(1,-2)到直线l:tx+y-t+1=0的最大值为1.
∴|AB|的最小值是2
| 9-1 |
| 2 |
故答案为:4,4
| 2 |
点评:本题考查了简单曲线的极坐标方程,考查了直线和圆的位置关系,是基础题.

练习册系列答案
相关题目
已知命题p:A={x||x-a|<4},q:B={x|(x-2)(3-x)>0},若非p是非q的充分条件,则实数a的取值范围是( )
| A、(-1,6) |
| B、[-1,6] |
| C、(-∞,-1)∪(6,+∞) |
| D、(-∞,-1]∪[6,+∞) |
 已知某正三棱锥的三视图如图所示,其中正视图是边长为2的正三角形,则该正三棱锥的体积为
已知某正三棱锥的三视图如图所示,其中正视图是边长为2的正三角形,则该正三棱锥的体积为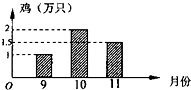 为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区9月份至11月份注射疫苗的所有养鸡场进行了调查.表格表示每个月所调查的养鸡场的个数,如图表示三个月中各养鸡场注射了疫苗的鸡的数量的平均数.根据图表提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为
为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区9月份至11月份注射疫苗的所有养鸡场进行了调查.表格表示每个月所调查的养鸡场的个数,如图表示三个月中各养鸡场注射了疫苗的鸡的数量的平均数.根据图表提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为