题目内容
已知三棱锥S-ABC中,SA=SB=SC=2,AB=AC=BC=3,则侧棱SA与底面ABC所成角的大小为 .
考点:直线与平面所成的角
专题:空间角
分析:首先根据已知条件,证得三棱锥为正三棱锥,进一步做出线面的夹角,最后利用解直角三角形知识求出结果.
解答:
解:已知三棱锥S-ABC中,SA=SB=SC=2,AB=AC=BC=3,
则:三棱锥S-ABC为正三棱锥.
过S点向底面ABC做垂线,垂足为O,则点O为△ABC的中心.
进一步解得:AO=
由于:△SOA是直角三角形.
则;进一步解得:SO=1
则:tan∠SAO=
=
解得:∠SAO=30°
故答案为:30°

则:三棱锥S-ABC为正三棱锥.
过S点向底面ABC做垂线,垂足为O,则点O为△ABC的中心.
进一步解得:AO=
| 3 |
由于:△SOA是直角三角形.
则;进一步解得:SO=1
则:tan∠SAO=
| SO |
| AO |
| ||
| 3 |
解得:∠SAO=30°
故答案为:30°

点评:本题考查的知识要点:正三棱锥的应用,线面夹角的应用.属于基础题型.

练习册系列答案
相关题目
如图,平行四边形ABCD的对角线交点是O,则下列等式成立的是( )
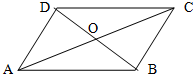

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
圆x2+2x+y2+4y-1=0上到直线x+y+1=0的距离为
的点共有( )
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
在四面体ABCD中,已知棱AC的长度为
,其余各棱长都为1,则二面角B-AC-D的大小为( )
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |