题目内容
18.在平行四边形ABCD中,O是对角线的交点,$\overrightarrow{CE}$=-3$\overrightarrow{DE}$,则( )| A. | $\overrightarrow{OE}$=-$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | B. | $\overrightarrow{OE}$=-$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AD}$ | C. | $\overrightarrow{OE}$=$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{4}$$\overrightarrow{AD}$ | D. | $\overrightarrow{OE}$=$\frac{1}{4}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{AD}$ |
分析 由题意知$\overrightarrow{CE}$=-$\frac{3}{4}$$\overrightarrow{AB}$,$\overrightarrow{OC}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AD}$),从而求$\overrightarrow{OE}$.
解答  解:∵$\overrightarrow{CE}$=-3$\overrightarrow{DE}$,
解:∵$\overrightarrow{CE}$=-3$\overrightarrow{DE}$,
∴$\overrightarrow{CE}$=$\frac{3}{4}$$\overrightarrow{CD}$=-$\frac{3}{4}$$\overrightarrow{AB}$,
∴$\overrightarrow{OC}$=$\frac{1}{2}$$\overrightarrow{AC}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AD}$),
∴$\overrightarrow{OE}$=$\overrightarrow{OC}$+$\overrightarrow{CE}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AD}$)-$\frac{3}{4}$$\overrightarrow{AB}$═$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{4}$$\overrightarrow{AD}$,
故选C.
点评 本题考查了平面向量线性运算的应用及数形结合的思想方法应用.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
13.成等差数列的三个正数的和等于6,并且这三个数分别加上3、6、13后成为等比数列{bn}中的b3、b4、b5,则数列{bn}的通项公式为( )
| A. | bn=2n-1 | B. | bn=3n-1 | C. | bn=2n-2 | D. | bn=3n-2 |
10.设Sn是等差数列{an}的前n项和,若a1=-16,公差为2.那么使Sn取得最小值的n等于( )
| A. | 8 | B. | 8或9 | C. | 9或10 | D. | 7 |
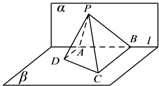 如图,已知平面α⊥β,α∩β=l,A,B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,AD=3,AB=6,CB=6,P是平面α上的一动点,且直线PD,PC与平面α所成角相等,则二面角P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$.
如图,已知平面α⊥β,α∩β=l,A,B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,AD=3,AB=6,CB=6,P是平面α上的一动点,且直线PD,PC与平面α所成角相等,则二面角P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$.