题目内容
写出数列的一个通项公式,使它的前4项分别是下列各数:
(1)
,
,
,
;
(2)1+
,1-
,1+
,1-
;
(3)7,77,777,7777;
(4)0,
,0,
.
(1)
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 8 |
| 7 |
| 16 |
(2)1+
| 1 |
| 22 |
| 3 |
| 42 |
| 5 |
| 62 |
| 7 |
| 82 |
(3)7,77,777,7777;
(4)0,
| 2 |
| 2 |
考点:数列的概念及简单表示法
专题:点列、递归数列与数学归纳法
分析:根据各组数列的前四项特征,写出符合条件的通项公式即可,通项公式也不是唯一的.
解答:
解:(1)∵
,
,
,
,
观察每一项的分子是连续的奇数,分母是2n,
∴an=
,n∈N*;
(2)∵1+
,1-
,1+
,1-
,
观察每一项的组成是1加或减一个分数的形式,
分数的分子是连续的奇数,分母是连续偶数的平方,
∴an=1+(-1)n+1•
,n∈N*;
(3)∵7,77,777,7777,
∴该数列可化为
(10-1),
(100-1),
(1000-1),
(10000-1),
∴an=
(10n-1),n∈N*;
(4)∵0,
,0,
,
∴该数列可化为(1-1)•
,(1+1)•
,(1-1)•
,(1+1)•
;
∴an=[1-(-1)n]•
,n∈N*.
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 8 |
| 7 |
| 16 |
观察每一项的分子是连续的奇数,分母是2n,
∴an=
| 2n-1 |
| 2n |
(2)∵1+
| 1 |
| 22 |
| 3 |
| 42 |
| 5 |
| 62 |
| 7 |
| 82 |
观察每一项的组成是1加或减一个分数的形式,
分数的分子是连续的奇数,分母是连续偶数的平方,
∴an=1+(-1)n+1•
| 2n-1 |
| (2n)2 |
(3)∵7,77,777,7777,
∴该数列可化为
| 7 |
| 9 |
| 7 |
| 9 |
| 7 |
| 9 |
| 7 |
| 9 |
∴an=
| 7 |
| 9 |
(4)∵0,
| 2 |
| 2 |
∴该数列可化为(1-1)•
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴an=[1-(-1)n]•
| ||
| 2 |
点评:本题考查了数列的通项公式的应用问题,解题时应根据数列的各项特征,归纳数列的通项公式,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,ABCD-A1B1C1D1为正方体,异面直线AD与CB1所成的角是( )


| A、30° | B、45° |
| C、60° | D、90° |
 如图,在直三棱柱ABC-A1B1C1中,AA1=4,AB=5,BC=3,AC=4,D、E分半为CC1、AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AA1=4,AB=5,BC=3,AC=4,D、E分半为CC1、AB的中点.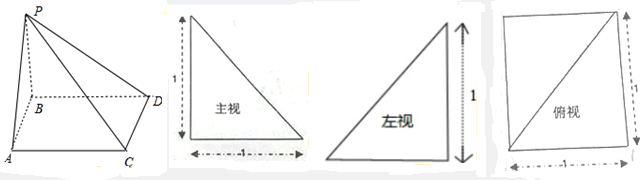 (1)求四棱锥的体积和表面积;
(1)求四棱锥的体积和表面积;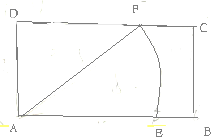 如图,矩形ABCD两邻边长分别为AB=6,AD=3,以A为圆心,5为半径画圆交AB于E,交CD于F,定义点集I={P|AP≤5}
如图,矩形ABCD两邻边长分别为AB=6,AD=3,以A为圆心,5为半径画圆交AB于E,交CD于F,定义点集I={P|AP≤5}