题目内容
规定函数y=f(x)图象上的点到坐标原点距离的最小值叫做函数y=f(x)的“中心距离”,给出以下四个命题:
①函数y=
的“中心距离”大于1;
②函数y=
的“中心距离”大于1;
③若函数y=f(x)(x∈R)与y=g(x)(x∈R)的“中心距离”相等,则函数h(x)=f(x)-g(x)至少有一个零点.
以上命题是真命题的序号是 .
①函数y=
| 1 |
| x |
②函数y=
| -x2-4x+5 |
③若函数y=f(x)(x∈R)与y=g(x)(x∈R)的“中心距离”相等,则函数h(x)=f(x)-g(x)至少有一个零点.
以上命题是真命题的序号是
考点:进行简单的合情推理
专题:推理和证明
分析:①②利用新定义,计算函数y=f(x)图象上的点到坐标原点距离的最小值,即可判定,③取特例可判断真假.
解答:
解:①函数y=
图象上的点到原点距离d=
≥
>1,即函数y=
的“中心距离”大于1,正确;
②函数y=
的定义域为:[-5,1],其图象上的点到原点距离d=
=
≥1,错误;
③取函数y=f(x)=x2+1,y=g(x)=-x2-1,函数h(x)=f(x)-g(x)=2x2+2,没有零点,错误.
故正确命题的序号只有:①,
故答案为:①
| 1 |
| x |
x2+
|
| 2 |
| 1 |
| x |
②函数y=
| -x2-4x+5 |
| x2+(-x2-4x+5) |
| -4x+5 |
③取函数y=f(x)=x2+1,y=g(x)=-x2-1,函数h(x)=f(x)-g(x)=2x2+2,没有零点,错误.
故正确命题的序号只有:①,
故答案为:①
点评:本题考查新定义,考查距离的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知椭圆
+
=1(a>b>0)的左顶点为A,左焦点为F,上顶点为B,且∠BAO+∠BFO=90°(O为坐标原点),则椭圆的离心率e=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
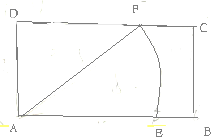 如图,矩形ABCD两邻边长分别为AB=6,AD=3,以A为圆心,5为半径画圆交AB于E,交CD于F,定义点集I={P|AP≤5}
如图,矩形ABCD两邻边长分别为AB=6,AD=3,以A为圆心,5为半径画圆交AB于E,交CD于F,定义点集I={P|AP≤5}