题目内容
6.在△ABC中,B=60°,C=45°,BC=8,D为BC上一点,AD=4(3$-\sqrt{3}$),$\overrightarrow{BD}$=$λ\overrightarrow{BC}$,则λ的值为( )| A. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{2-\sqrt{3}}{2}$ |
分析 使用正弦定理求出AB,则$\overrightarrow{AD}=\overrightarrow{AB}+λ\overrightarrow{BC}$,两边平方得出关于λ的方程,解出λ即可.
解答 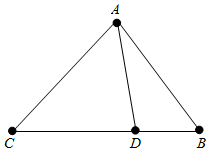 解:∠BAC=180°-B-C=75°,∴sin∠BAC=$\frac{\sqrt{6}+\sqrt{2}}{4}$,在△ABC中,由正弦定理得:$\frac{BC}{sin∠BAC}=\frac{AB}{sinC}$,即
解:∠BAC=180°-B-C=75°,∴sin∠BAC=$\frac{\sqrt{6}+\sqrt{2}}{4}$,在△ABC中,由正弦定理得:$\frac{BC}{sin∠BAC}=\frac{AB}{sinC}$,即
∴AB=$\frac{BC•sinC}{sin∠BAC}$=$\frac{8×\frac{\sqrt{2}}{2}}{\frac{\sqrt{6}+\sqrt{2}}{4}}$=8($\sqrt{3}-1$).
∴$\overrightarrow{AB}•\overrightarrow{BC}=8(\sqrt{3}-1)×8×cos120°$=32(1-$\sqrt{3}$).
∵$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AB}+λ\overrightarrow{BC}$,
∴${\overrightarrow{AD}}^{2}$=${\overrightarrow{AB}}^{2}+2λ\overrightarrow{AB}•\overrightarrow{BC}+{λ}^{2}{\overrightarrow{BC}}^{2}$,
即16(3-$\sqrt{3}$)2=64($\sqrt{3}-1$)2+64λ(1-$\sqrt{3}$)+64λ2,
∴2λ2+2(1-$\sqrt{3}$)λ+2-$\sqrt{3}=0$,
解得λ=$\frac{\sqrt{3}-1}{2}$.
故选:C.
点评 本题考查了正弦定理,平面向量的数量积运算,属于中档题.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案| A. | 2014 | B. | 2017 | C. | 2015 | D. | 2016 |
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | $\frac{9}{2}$ |
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
| A. | $\frac{n(n+1)}{2}$ | B. | $\frac{{n}^{2}-n+2}{2}$ | C. | 2n2-n | D. | 2n-1 |