题目内容
10.三棱锥P-ABC的四个顶点都在半径为4的球面上,且三条侧棱两两互相垂直,则该三棱锥侧面积的最大值为32.分析 由已知,三棱锥P-ABC的四个顶点均在半径为3的球面上,且PA,PB,PC两两垂直,球直径等于以PA,PB,PC为棱的长方体的对角线,由基本不等式易得到三棱锥P-ABC的侧面积的最大值.
解答 解:∵PA,PB,PC两两垂直,
又∵三棱锥P-ABC的四个顶点均在半径为3的球面上,
∴以PA,PB,PC为棱的长方体的对角线即为球的一条直径.
∴64=PA2+PB2+PC2,
则由基本不等式可得PA2+PB2≥2PA•PB,PA2+PC2≥2PA•PC,PB2+PC2≥2PB•PC,
即64=PA2+PB2+PC2≥PA•PB+PB•PC+PA•PC
则三棱锥P-ABC的侧面积S=$\frac{1}{2}$(PA•PB+PB•PC+PA•PC)≤32,
则三棱锥P-ABC的侧面积的最大值为32,
故答案为:32.
点评 本题考查的知识点是棱锥的侧面积,基本不等式,棱柱的外接球,其中根据已知条件,得到棱锥的外接球直径等于以PA,PB,PC为棱的长方体的对角线,是解答本题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
20.函数y=xcosx-sinx的部分图象大致为( )
| A. | 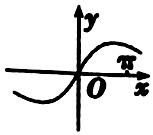 | B. |  | ||
| C. | 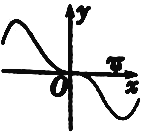 | D. | 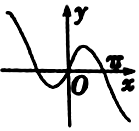 |
1.复数z=$\frac{1+i}{i}$,则|z|=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | -$\sqrt{2}$ | D. | 1-i |
2.已知全集A={x|x≤9,x∈N*}集合B={x|0<x<7},则A∩B=( )
| A. | {x|0<x<7} | B. | {x|1≤x≤6} | C. | {1,2,3,4,5,6} | D. | {7,8,9} |
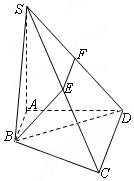 如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.
如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.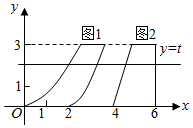 我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容 异”.“势’’即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为l的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图l和图2所截得的两线段长始终相等,则图l的面积为$\frac{9}{2}$.
我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容 异”.“势’’即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为l的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图l和图2所截得的两线段长始终相等,则图l的面积为$\frac{9}{2}$.