题目内容
15．
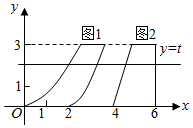我国南北朝时代的数学家祖暅提出体积的计算原理（祖暅原理）：“幂势既同，则积不容 异”．“势’’即是高，“幂”是面积．意思是：如果两等高的几何体在同高处截得两几何体的截面积恒等，那么这两个几何体的体积相等，类比祖暅原理，如图所示，在平面直角坐标系中，图1是一个形状不规则的封闭图形，图2是一个上底为l的梯形，且当实数t取[0，3]上的任意值时，直线y=t被图l和图2所截得的两线段长始终相等，则图l的面积为$\frac{9}{2}$．
分析 根据祖暅原理，可得图1的面积=梯形的面积，即可得出结论．
解答 解：根据祖暅原理，可得图1的面积=梯形的面积=$\frac{（1+2）×3}{2}$=$\frac{9}{2}$．
故答案为$\frac{9}{2}$．
点评 此题考查了梯形的面积公式，还考查了学生空间的想象能力及计算技能．
练习册系列答案
相关题目
6．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，且F2为抛物线y2=24x的焦点，设点P为两曲线的一个公共点，若△PF1F2的面积为36$\sqrt{6}$，则双曲线的方程为（ ）
| A． | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{27}$=1 | B． | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{9}$=1 | C． | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | D． | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 |
7．已知向量$\overrightarrow{a}$=（-2，4），$\overrightarrow{b}$=（-1，m）．若$\overrightarrow{a}$∥$\overrightarrow{b}$，则实数m的值为（ ）
| A． | -$\frac{1}{2}$ | B． | -2 | C． | 2 | D． | $\frac{1}{2}$ |
4．设集合M={-4，-3，-2，-1，0，1}，N={x∈R|x2+3x＜0}，则M∩N=（ ）
| A． | {-3，-2，-1，0} | B． | {-2，-1，0} | C． | {-3，-2，-1} | D． | {-2，-1} |
5．从1、2、3、4、5、6中任三个数，则所取的三个数按一定的顺序可排成等差数列的概率为（ ）
| A． | $\frac{3}{10}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{7}{20}$ |