题目内容
已知函数f（x）=Asin（x+
），x∈R，且f（
）=
．
（1）求A的值；
（2）若f（θ）+f（-θ）=
，θ∈（0，
），求f（
-θ）．
| π |
| 4 |
| 5π |
| 12 |
| 3 |
| 2 |
（1）求A的值；
（2）若f（θ）+f（-θ）=
| 3 |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,两角和与差的正弦函数
专题：三角函数的图像与性质
分析：（1）由函数f（x）的解析式以及f（
）=
，求得A的值．
（2）由（1）可得 f（x）=
sin（x+
），根据f（θ）+f（-θ）=
，求得cosθ 的值，再由 θ∈（0，
），求得sinθ 的值，从而求得f（
-θ） 的值．
| 5π |
| 12 |
| 3 |
| 2 |
（2）由（1）可得 f（x）=
| 3 |
| π |
| 4 |
| 3 |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
解答：
解：（1）∵函数f（x）=Asin（x+
），x∈R，且f（
）=
．
∴Asin（
+
）=Asin
=A•
=
，
∴A=
．
（2）由（1）可得 f（x）=
sin（x+
），
∴f（θ）+f（-θ）=
sin（θ+
）+
sin（-θ+
）=2
sin
cosθ=
cosθ=
，
∴cosθ=
，再由 θ∈（0，
），可得sinθ=
．
∴f（
-θ）=
sin（
-θ+
）=
sin（π-θ）=
sinθ=
．
| π |
| 4 |
| 5π |
| 12 |
| 3 |
| 2 |
∴Asin（
| 5π |
| 12 |
| π |
| 4 |
| 2π |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
∴A=
| 3 |
（2）由（1）可得 f（x）=
| 3 |
| π |
| 4 |
∴f（θ）+f（-θ）=
| 3 |
| π |
| 4 |
| 3 |
| π |
| 4 |
| 3 |
| π |
| 4 |
| 6 |
| 3 |
| 2 |
∴cosθ=
| ||
| 4 |
| π |
| 2 |
| ||
| 4 |
∴f（
| 3π |
| 4 |
| 3 |
| 3π |
| 4 |
| π |
| 4 |
| 3 |
| 3 |
| ||
| 4 |
点评：本题主要考查三角函数的恒等变换，同角三角函数的基本关系，属于中档题．
练习册系列答案
相关题目
设α∈（0，
），β∈（0，
），且tanα=
，则（ ）
| π |
| 2 |
| π |
| 2 |
| 1+sinβ |
| cosβ |
A、3α-β=
| ||
B、3α+β=
| ||
C、2α-β=
| ||
D、2α+β=
|
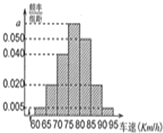2014年“五一节”期间，高速公路车辆较多，交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度，采用的方法是：按到达监控点先后顺序，每隔50辆抽取一辆，总共抽取120辆，分别记下其行车速度，将行车速度（km/h）分成七段[60，65），[65，70），[70，75），[75，80），[80，85），[85，90），[90，95）后得到如图所示的频率分布直方图，据图解答下列问题：