题目内容
12．已知函数f（x）在区间（-1，0）和（1，+∞）上递增，在区间（-∞，-1）和（0，1）上递减，则f（x）的解析式可以是f（x）=|x2-1|．（只需写出一个符合题意的解析式）分析 根据函数单调性的性质求出函数的解析式即可．
解答 解：若函数f（x）在区间（-1，0）和（1，+∞）上递增，在区间（-∞，-1）和（0，1）上递减，
则函数的解析式可以是：f（x）=|x2-1|，
故答案为：f（x）=|x2-1|．
点评 本题考查了函数的单调性问题，考查常见函数的性质，是一道基础题．
练习册系列答案
相关题目
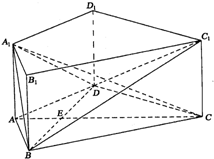如图，在直四棱柱ABCD-A1B1C1D1中，AB=AD=2，DC=2$\sqrt{3}$，AA1=$\sqrt{3}$，AD⊥DC，AC⊥BD，垂足为E，
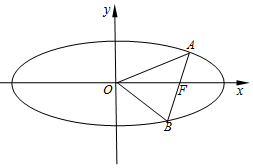如图，在平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦距为2，过右焦点F的直线l交椭圆于A、B两点，当l与x轴垂直时，AB长为$\frac{{4\sqrt{3}}}{3}$．
17．已知集合A={0，2，4，6}，B={x∈N|2x≤33}，则集合A∩B的子集个数为（ ）
| A． | 6 | B． | 7 | C． | 8 | D． | 4 |
4．已知集合M={x|y=ln（x2-3x-4）}，N={y|y=2x-1}，则M∩N等于（ ）
| A． | {x|x＞4} | B． | {x|x＞0} | C． | {x|x＜-1} | D． | {x|x＞4或x＜-1} |