题目内容
14．已知函数f（x）=x2+bx+c，且f（1+x）=f（-x），则f（-2）、f（0）、f（2）的大小关系是f（-2）＞f（2）＞f（0）．分析 由f（1+x）=f（-x）可知f（x）的对称轴为x=$\frac{1}{2}$，分别计算出三个数比较大小即可．
解答 解：∵f（1+x）=f（-x），∴f（x）的对称轴为x=$\frac{1}{2}$，∴b=-1，∴f（x）=x2-x+c．
∴f（-2）=6+c，f（0）=c，f（2）=2+c，∴f（-2）＞f（2）＞f（0）．
故答案为f（-2）＞f（2）＞f（0）．
点评 本题考查了二次函数的对称性，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
4．已知双曲线中心在原点且一个焦点为F1$（-\sqrt{5}{，^{\;}}0）$，点P位于该双曲线上，线段PF1的中点坐标为（0，2），则双曲线的方程为（ ）
| A． | $\frac{{x}^{2}}{2}$-y2=1 | B． | ${x^2}-\frac{y^2}{4}=1$ | C． | $\frac{x^2}{2}-\frac{y^2}{3}=1$ | D． | $\frac{x^2}{3}-\frac{y^2}{2}=1$ |
5．设a，b∈R，则“a＞b＞0”是“$\frac{1}{a}$$＜\frac{1}{b}$”的（ ）条件．
| A． | 充分而不必要 | B． | 必要而不充分 | ||
| C． | 充分必要 | D． | 既不充分也不必要 |
6．
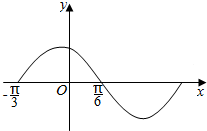函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的部分图象如图所示，如果x1，x2∈（-$\frac{π}{3}$，$\frac{π}{6}$），且f（x1）=f（x2），则f（x1+x2）等于（ ）
函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的部分图象如图所示，如果x1，x2∈（-$\frac{π}{3}$，$\frac{π}{6}$），且f（x1）=f（x2），则f（x1+x2）等于（ ）| A． | -1 | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | 1 |
4．$\sqrt{1-2sin（π+2）cos（π-2）}$等于（ ）
| A． | sin2-cos2 | B． | sin2+cos2 | C． | ±（sin2-cos2） | D． | cos2-sin2 |