题目内容
5．设a，b∈R，则“a＞b＞0”是“$\frac{1}{a}$$＜\frac{1}{b}$”的（ ）条件．| A． | 充分而不必要 | B． | 必要而不充分 | ||
| C． | 充分必要 | D． | 既不充分也不必要 |
分析 根据充分条件和必要条件的定义结合不等式的性质进行判断即可．
解答 解：若a＞b＞0，则$\frac{1}{a}$$＜\frac{1}{b}$成立，即充分性成立，
若a=-1，b=1，满足$\frac{1}{a}$$＜\frac{1}{b}$，但a＞b＞0不成立，即必要性不成立，
故“a＞b＞0”是“$\frac{1}{a}$$＜\frac{1}{b}$”的充分不必要条件，
故选：A
点评 本题主要考查充分条件和必要条件的判断，根据不等式的关系是解决本题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
15．已知a、b、c分别为△ABC三个内角A、B、C所对的边长，∠A=60°，且acosB-bcosA=$\frac{3}{5}$c，则$\frac{2absinC}{{a}^{2}+{b}^{2}-{c}^{2}}$=（ ）
| A． | -5$\sqrt{3}$ | B． | -4$\sqrt{3}$ | C． | 4$\sqrt{3}$ | D． | 5$\sqrt{3}$ |
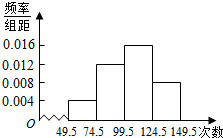为了调查学生的课外阅读情况，在某班级对全体学生每天阅读时间（单位：分钟）进行调查，将调查数据整理后，画出频率分布直方图如图，已知图中从左到右前三个小组的频率分别是0.1，0.3，0.4，第三组的频数为20．
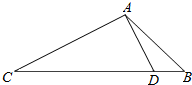如图△ABC中，已知点D在BC边上，且AD⊥AC，sin∠BAC=$\frac{{2\sqrt{2}}}{3}$，AB=3$\sqrt{2}$，BD=$\sqrt{3}$．